A geometria plana é a área da matemática que estuda as figuras bidimensionais, isto é, com duas dimensões.
As figuras planas são figuras dispostas no plano, possuindo duas medidas que são o comprimento e a largura.
A geometria plana foi criada pelo matemático Euclides de Alexandria, com base nos axiomas e postulados propostos por ele. Por esse motivo, a geometria plana também é chamada geometria euclidiana.
Conceitos Básicos da Geometria Plana
No estudo da geometria plana alguns conceitos são aceitos sem que precisamos provar. Esses conceitos são chamados de primitivos ou axiomas, aceito na matemática sem a necessidade de demonstrações. São eles:
Ponto
O ponto é representado na geometria por letras maiúsculas sendo definido por Euclides como algo que não possui partes nem dimensões.
Reta
A reta é formada por pontos reunidos formando uma linha, sem largura e com comprimento. A reta é infinita para os dois sentidos. Representamos uma reta na geometria por letras minúsculas.
As retas podem ser apresentadas nas seguintes posições:
- Vertical;
- Horizontal;
- Inclinada.

Existem alguns conceitos que também são estudados na geometria plana envolvendo as retas:
- Retas Concorrentes: são retas que se cruzam em um ponto em comum;
- Retas Paralelas: são retas que não se cruzam e estão a uma mesma distância no plano para todos os pontos.
Plano
O plano é formado por uma superfície que contém todos os pontos e retas. O plano possui duas dimensões: comprimento e largura. É representado na geometria por letras do alfabeto grego.
Segmento de Reta
O segmento de reta é a parte de uma reta que está compreendida entre dois pontos da reta. É finito, ou seja, possui início e fim. E é sempre representado por duas letras maiúsculas com um traço em cima.
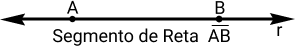
Semirreta
A semirreta possui início em um ponto da reta e é infinita para uma das suas direções. É representada na geometria por duas letras maiúsculas com uma seta em cima indicando a direção.

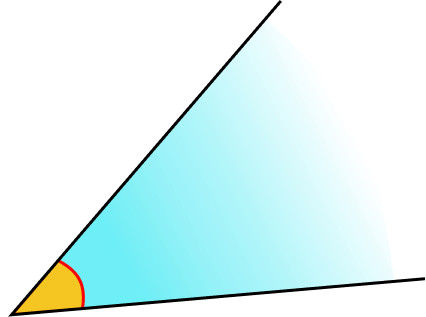
Ângulos
O ângulo é a região compreendida entre dois segmentos de retas que possuem um mesmo ponto em comum. Os ângulos são medidos em graus ou radianos. Essa medida é a abertura entre os dois segmentos de retas.
Área
Área é uma medida usada para definir o tamanho da superfície de uma figura. A área é calculada usando as medidas de comprimento e largura das figuras geométricas.
Leia mais sobre como calcular a área de figuras planas:
Perímetro
O perímetro é a medida equivalente à soma das medidas dos lados de uma figura geométrica.
Lei mais sobre como calcular o perímetro:
Figuras da Geometria Plana
A geometria plana estuda diversas figuras planas, as principais são: triangulo, quadrado, retângulo, circulo, circunferência, trapézio e losango. As figuras planas são chamadas na geometria por polígonos. Polígonos são figuras planas e fechadas.
Triângulo
O triângulo é uma figura plana formada por três lados. Os lados são segmentos de retas unidos nos vértices.
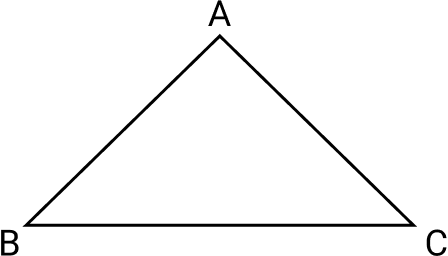
Os triângulos são classificados quanto aos lados em: triângulo equilátero, isósceles e escaleno.
- Triângulo Equilátero: triângulo com todos os lados e ângulos internos congruentes;
- Triângulo Isósceles: triângulo que possui dois lados e dois ângulos internos congruentes;
- Triângulo Escaleno: triângulo em que todas as medidas diferem;
Os triângulos também são classificados quanto aos ângulos em: triângulo retângulo, obtusângulo e acutângulo.
- Triângulo Retângulo: triângulo que possui um ângulo de 90°;
- Triângulo Obtusângulo: triângulo que possui um ângulo interno obtuso (maior que 90°);
- Triângulo Acutângulo: triângulo que todos os ângulos internos são menores que 90°.
Ainda sobre os triângulos, estude mais sobre o assunto:
- Área do Triângulo
- Perímetro do Triângulo
- Semelhança de Triângulos
- Triângulo Retângulo
- Triângulo Equilátero
- Triângulo Escaleno
- Triângulo Isósceles
- Trigonometria no Triângulo Retângulo
Quadrado
O quadrado é um paralelogramo formado por quatro lados, dois a dois paralelos e com ângulos internos congruentes e retos (90°).

Leia também:
Retângulo
O retângulo é um paralelogramo com lados dois a dois congruentes e paralelos. Os ângulos internos são congruentes e retos (90°).

Leia também:
Círculo
O círculo é uma figura plana limitada pela circunferência, e corresponde ao espaço interno formado pelo conjunto de todos os pontos do plano. Também é chamado disco.

Leia também:
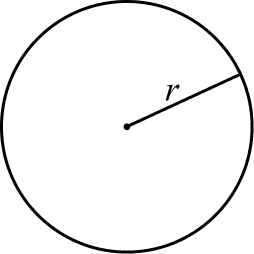
Circunferência
A circunferência é formada por um conjunto de pontos a uma mesma distância do centro equivalente à medida do raio.
Trapézio
O trapézio é um polígono formado por duas bases paralelas e com medidas diferentes. A base de menor medida é chamada “base menor”, a base de maior medida é chamada “base maior”.

O trapézio pode ser classificado de acordo a medida dos lados e do ângulo em: trapézio retângulo, isósceles e escaleno.
- Trapézio Retângulo: quando o trapézio possui dois ângulos internos de 90°;
- Trapézio Isósceles: quando os lados que não são bases são congruentes;
- Trapézio Escaleno: quando todos os lados possuem medidas diferentes.
Leia mais sobre o assunto:
Losango
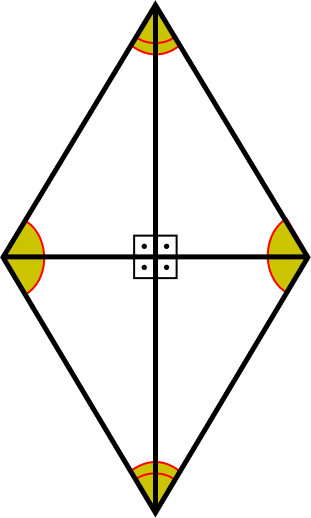
O losango é um paralelogramo formado por quatro lados, com lados opostos paralelos e congruentes. Os ângulos opostos também são congruentes.
Leia também:
Geometria Espacial
A geometria espacial estuda as figuras com três dimensões, a saber: largura, comprimento e altura. Na geometria espacial é estudado o conceito de volume, sendo a medida de capacidade dos sólidos geométricos.
Exercícios
Acesse e veja os exercícios no link a seguir:
Leia o artigo sobre geometria espacial:


