Treine seus conhecimentos respondendo os exercícios de vestibulares e ENEM abaixo sobre geometria plana.
1) (UPF/2009) Se os ângulos externos de um polígono regular medem 18°, então o número de diagonais desse polígono é:
a) 190
b) 170
c) 120
d) 135
e) 162
Ver resposta
Para encontrar o número de diagonais temos que saber quantos lados possui esse polígono. Sabendo que a soma dos ângulos externos de um polígono é 360º, assim 360°/18° = 20.
Dessa forma, sabemos que o polígono em questão é um icosaedro, pois possui 20 lados.
O número de diagonais de um polígono pode ser calculado utilizando a seguinte fórmula:
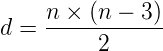
Onde n é o total de lados do polígono.
Portanto,
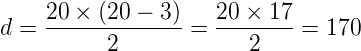
2) (UNISC INV/2014) Os lados de um losango medem 4 cm e um de seus ângulos 60º. As medidas da diagonal menor e da diagonal maior do losango medem, respectivamente,
a) 2 cm e 2√3 cm.
b) 2√3 cm e 4 cm.
c) 2√3 cm e 4√3 cm.
d) 4 cm e 4√3 cm.
e) 4 cm e 8 cm.
Ver resposta
Sabemos que um losango possui lados congruentes e ângulos opostos também congruentes.
Os ângulos internos do losango dois são agudos e dois obtusos, então 60° corresponde aos ângulos agudos.
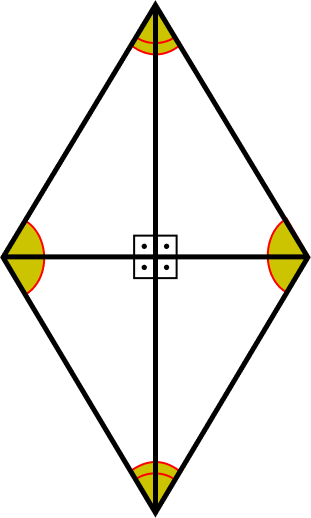
As diagonais são as bissetrizes dos ângulos, elas se interceptam formando quatro triângulos retângulos.
Assim, chamando x a medida da metade da diagonal menor e y a metade da diagonal maior, temos que:
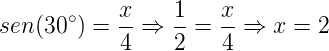
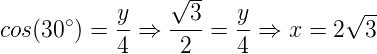
Agora basta multiplicar o resultado de x e y por 2 e teremos as medidas da diagonal menor e maior, respectivamente.
Logo:
d = 2 . 2 = 4 cm
D = 2 . 2√3 = 4√3 cm
Portanto, resposta D.
3) (UERJ/2015) Uma chapa de aço com a forma de um setor circular possui raio R e perímetro 3R, conforme ilustra a imagem.
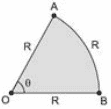
A área do setor equivale a:
a) R²
b) R²/4
c) R²/2
d) 3R²/2
Ver resposta
A área do setor circular aumenta proporcionalmente ao crescimento do arco. Sendo assim, a área do setor circular é proporcional a área de um círculo.
Então, temos a seguinte proporção:
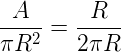
Então, a área do setor circular é:
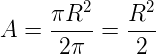
Portanto, resposta C.
4) Sabendo que o segmento AB mede 20 cm, calcule o valor de x.
a) 
b) 
Ver resposta
a) x = 20 – 4 = 16 cm
b) x = 20 – 17 = 3 cm
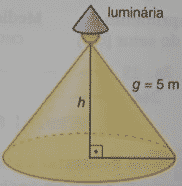
5) (ENEM 2010) Um arquiteto está fazendo um projeto de iluminação de ambiente e necessita saber a altura que deverá instalar a luminária ilustrada na figura. Sabendo-se que a luminária deverá iluminar uma área circular de 28,26 m², considerando π = 3,14, a altura h será igual a:
a) 3 m
b) 4 m
c) 5 m
d) 9 m
e) 16 m
Ver resposta
Temos os seguintes dados:
Área circular: 28,26 m²
geratriz: 5 m
π = 3,14
Sabendo que a área circular é calculada pela fórmula: A = π . r²
Substituindo, temos:
28,26 = 3,14 . r²
28,26 / 3,14 = r²
r = √9 = 3 m
Agora que temos o valor do raio podemos utilizar o teorema de Pitágoras para encontrar a medida da altura, pois a altura mais a geratriz e o raio formam um triângulo retângulo.
Logo:
g² = h² + r² ⇒
5² = h² + 3² ⇒
25 = h² + 9 ⇒
25 – 9 = h² ⇒
h = √16 = 4 m
Portanto, a altura equivale a 4 m e a resposta da questão é a letra B.
Treinar é a melhor forma de aprender a resolver exercícios sobre geometria plana, portanto pratique.


