O Teorema de Pitágoras é um dos mais famosos teoremas da matemática. Este teorema é aplicado aos comprimentos dos lados do triângulo retângulo — triângulo que possui um ângulo reto, isto é, que mede 90°.
O Teorema de Pitágoras diz que: “O quadrado da medida da hipotenusa é igual à soma dos quadrados das medidas dos catetos”.
A hipotenusa é o lado do triângulo que tem a maior medida e fica oposta ao ângulo reto, enquanto os catetos existem dois: o cateto adjacente e o cateto oposto. O cateto adjacente é aquele que fica ao lado de um ângulo e o cateto oposto fica em frente a um determinado ângulo. Veja no triângulo abaixo:

Hipotenusa: a hipotenusa é o lado que fica oposto ao ângulo reto.
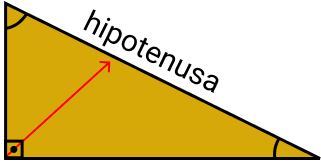
Cateto Oposto: o cateto oposto fica oposto a um dos ângulos.

Cateto Adjacente: o cateto adjacente fica ao lado de um dos ângulos.
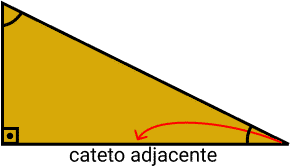
Fórmula do Teorema de Pitágoras
O teorema de Pitágoras diz que a soma dos quadrados dos catetos é igual à hipotenusa ao quadrado. Isso pode ser traduzido em uma fórmula:
a² = b² + c²
Onde:
- a: representa a hipotenusa;
- b e c: representa os catetos oposto e adjacente.
Exemplo:
Considere um triângulo com as seguintes medidas:
- Hipotenusa: 5 cm
- Cateto Adjacente: 4 cm
- Cateto Oposto: 3 cm
Aplicando o Teorema de Pitágoras, a soma dos quadrados dos catetos tem que ser igual à medida da hipotenusa ao quadrado, assim: a² = b² + c²
Então: 5² = 3² + 4² ⇒ 25 = 9 + 16 ⇒ 25 = 25
Podemos ver isso na imagem abaixo, onde temos 9 quadrados no cateto oposto e 16 no cateto adjacente. Somando-se os quadrados dos catetos, chegamos a soma dos quadrados que estão na hipotenusa.
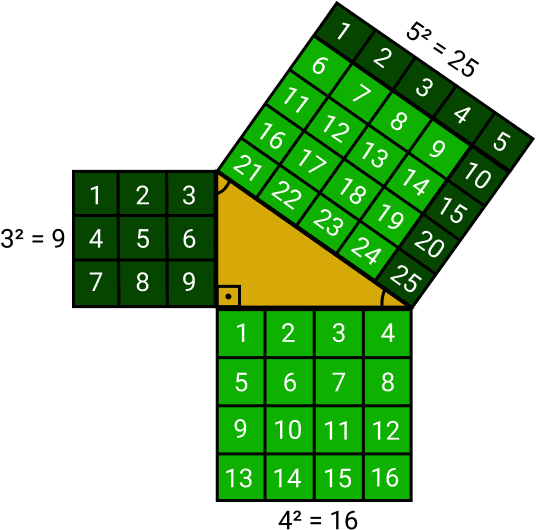
Pitágoras provou que a área dos quadrados construídos sobre os lados de um triângulo retângulo referente aos catetos, equivale à área do quadrado construído ao lado da hipotenusa.
Exercícios Resolvidos
Calcule a medida da hipotenusa para o triângulo retângulo ABC, com ângulo reto em B, sendo que os catetos AB e BC, têm medidas de 6 cm e 8 cm, respectivamente.

Cálculos dos quadrados dos catetos:
- (AB)² = 6² = 36 cm
- (BC)² = 8² = 64 cm
Aplicando o Teorema de Pitágoras, temos:
- (AC)² = (AB)² + (BC)²
- x² = 36 + 64, com x > 0 ⇔ x² = 100 ⇔ x = √100 ⇔ x = 10 cm
Calcule a medida do cateto AB do triângulo retângulo ABC, com ângulo reto em B, sabendo que a hipotenusa AC tem medida igual a 10 cm, e o cateto BC mede 5 cm.

Cálculo do quadrado da hipotenusa AC e do cateto BC:
- (AC)² = 10² = 100 cm
- (BC)² = 5² = 25 cm
Aplicando o Teorema de Pitágoras, temos:
- (AC)² = (BC)² + (AB)²
- 100 = 25 + x², com x > 0 ⇔ x² = 100 – 25 ⇔ x² = 75 cm ⇔ x = √75 ⇔ x = 5√3 cm
Exercícios Propostos
Acesse os exercícios propostos no link a seguir:



