O triângulo isósceles é uma categoria de triângulo que possui dois lados com as mesmas medidas. O lado com medida diferente dos demais lados é a base do triângulo. Além disso, os lados que têm as mesmas medidas formam um ângulo oposto a base do triângulo, esse ângulo é chamado ângulo do vértice.
Definição
Chamamos um triângulo de isósceles, se e somente se, ele possui dois lados congruentes.
Na matemática, a notação que representa a congruência entre dois lados é dado da seguinte forma:
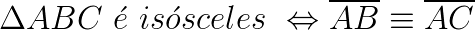
Exemplo:
Considere o triângulo ABC a seguir:

É um triângulo isósceles e os lados AB e AC possuem as mesmas medidas. A reta que parte do vértice A, dividindo o ângulo Â, é chamado de bissetriz. A bissetriz divide o triângulo em dois, formando dois triângulos retângulos, além de dividir o ângulo  em dois, também com a mesma medida.
A base do triângulo, formada pelo lado BC, é dividida ao meio pela bissetriz, assim as medidas de BD e CD são iguais.
Propriedades
Para o triângulo isósceles valem as seguintes propriedades:
- No triângulo isósceles os ângulos da base tem medidas iguais;
- A altura do triângulo isósceles tem a mesma medida da bissetriz do ângulo oposto a base.
Área dos Triângulos
Para calcular a área de um triângulo isósceles basta utilizarmos a fórmula geral para calcular a área de um triângulo.

Onde:
- A: representa a área do para o triângulo em questão;
- b: representa a base do triângulo;
- h: é a altura para o triângulo.
Exemplo:
Considere o triângulo a seguir, com medidas dos lados iguais a 10 cm, 10 cm e 12 cm.

Primeiramente, devemos encontrar a medida para a altura do triângulo, para isso devemos utilizar o Teorema de Pitágoras. Assim:

No triângulo isósceles, a medida da altura é a bissetriz que divide a base do triângulo na metade. Após encontrar o valor referente a altura, utilizamos a fórmula geral para qualquer triângulo e encontramos o valor referente a área para o triângulo apresentado.
Eixo Simetria
Como temos um triângulo isósceles, em que dois lados tem medidas iguais, se traçarmos uma reta a partir do ângulo Â, essa reta divide o triângulo ao meio formando dois triângulos com áreas idênticas. Essa reta é chamada Eixo de Simetria.
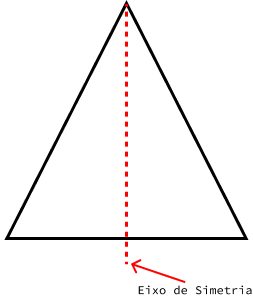
Se esse triângulo estivesse desenhado em um papel e recortássemos a figura do triângulo em relação ao seu lado, depois dobrássemos ele ao meio em relação ao Eixo de Simetria, às duas partes se coincidiriam.
Exercícios
Veja os exercícios acessando o link a seguir:



