A bissetriz é uma semirreta que inicia no vértice de um ângulo e o divide em dois ângulos com a mesma medida. É usada na geometria para analisar principalmente os triângulos.
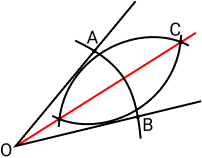
Na matemática, a bissetriz é definida como um lugar geométrico com pontos que equidistam duas retas concorrentes. Consequentemente, isto divide um ângulo em dois ângulos congruentes.
Tipos de Bissetrizes
Podemos classifica-las em dois tipos:
- Interna: é a semirreta que divide um ângulo interno qualquer;
- Externa: é a semirreta que divide o ângulo suplementar, ou seja, do ângulo externo. O ângulo suplementar é um ângulo que quando somado com o ângulo interno equivale a 180°.
Construção
Podemos construí-la para qualquer ângulo utilizando um compasso com os seguintes passos:
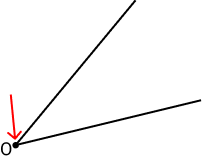
Coloque a ponta do compasso que não possui a grafite no vértice do ângulo:
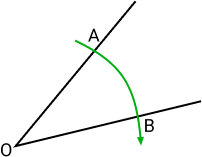
Desenhe um arco de forma que este arco corte os segmentos de retas OA e OB que formam o ângulo:
Coloque a ponta do compasso que não possui a grafite na intersecção em B e trace um novo arco, como na figura abaixo:
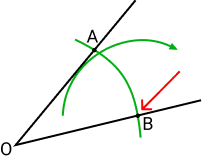
Faça o mesmo em A, trace o mesmo arco do passo anterior:
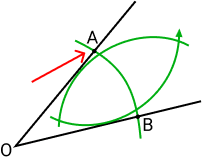
Agora trace uma semirreta do vértice do ângulo passando pelas intersecções dos arcos que acabamos de fazer:
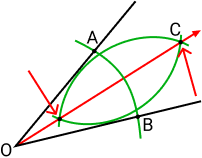
A bissetriz é a semirreta OC.
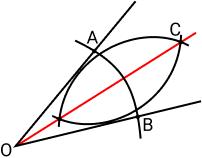
Teorema da Bissetriz Interna
Este teorema diz que ela divide o lado oposto ao ângulo em segmentos proporcionais aos lados adjacentes ao ângulo.
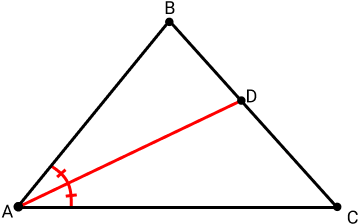
Isto quer dizer que se construirmos uma bissetriz para o triângulo ABC, temos que ela divide o lado BC do triângulo ABC de forma que o segmento AB é proporcional a BD e AC é proporcional a CD. Assim, temos a seguinte proporção:
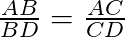
Essa proporção pode ser provada utilizando o Teorema de Tales.
Teorema da Bissetriz Externa
Este teorema externa diz que a bissetriz do ângulo externo de um triângulo divide o lado oposto em segmentos proporcionais aos lados adjacentes.
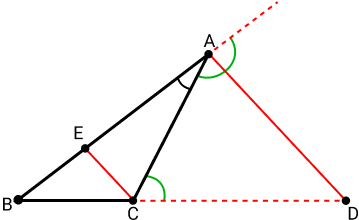
Isto quer dizer que se temos um triângulo ABC, a bissetriz do ângulo externo BAC, define a medida do segmento CD. Assim, se traçarmos a bissetriz do ângulo ACB, temos a formação de um ponto E no segmento AB.
Portanto, temos a seguinte proporção:
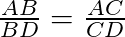
Essa proporção também pode ser provada utilizando o Teorema de Tales.
Propriedades
As bissetrizes possuem as seguintes propriedades:
- Dois ângulos opostos pelo vértice possuem bissetrizes opostas;
- Dois ângulos replementares possuem bissetrizes opostas;
- Dois ângulos suplementares possuem bissetrizes perpendiculares.
Exercícios
Veja os exercícios no link a seguir:



