Chamamos duas retas de concorrentes disposta no mesmo plano, quando às duas retas se cruzam em um ponto que é comum a ambas.
Um caso particular de retas concorrentes são as retas perpendiculares entre si. Elas se cruzam em um ponto comum e formam um angulo reto (ângulo de 90°).
As retas concorrentes são classificadas segundo os ângulos da seguinte forma:
Perpendiculares: quando forma um ângulo reto (ângulo que mede 90°);
Oblíquas: quando uma reta cruza a outra de forma não perpendicular.

Nas retas concorrentes oblíquas, os ângulos formados pelo cruzamento em um ponto comum às duas retas são diferentes de 90°. Dessa forma, não importa a medida do ângulo para ser oblíqua, ele só tem que ser diferente de 90°.
Duas retas concorrentes formam 4 ângulos entre si ao se cruzarem num ponto comum. A partir disso, podemos apresentar alguns conceitos em relação aos ângulos formados.
Análise dos Ângulos formados
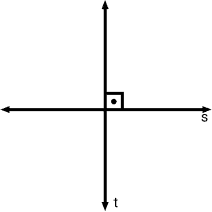
As retas concorrentes, ao se cruzarem em um ponto comum, formam 4 ângulos. Os ângulos opostos pelo vértice tem medidas iguais. Na imagem, os ângulos α e β são opostos entre si pelo vértice A e tem medidas iguais. O vértice é o ponto A onde as retas se cruzam.

Além disso, dois ângulos com medidas diferentes tem medidas de 180° e são chamados de ângulos suplementares. Na imagem, os ângulos α e β tem medidas diferentes e a soma das medidas dos ângulos devem medir 180°.

As retas concorrentes que são perpendiculares entre si, formam 4 ângulos com medidas iguais, todos os ângulos são retos, isto é, possuem medidas iguais a 90°.

Ponto de Intersecção
A própria definição das retas concorrentes dizem que duas retas são concorrentes se existem um ponto comum entre ambas. Isto quer dizer que elas se cruzam uma com a outra ou simplesmente dizemos que é onde temos o ponto de intersecção das retas.
Se tivermos duas retas s e t, concorrentes, de forma que as equações gerais dessas retas sejam aux + buy + cu = 0 e atx + bty + ct = 0.
Como as retas são concorrentes, então, ao representarmos no plano cartesiano, as retas terão um ponto P em comum.

Dessa forma, o conjunto solução para o sistema com as equações gerais para as retas no sistema cartesiano é o par ordenado (x0, y0), o ponto de intersecção das retas (s ∩ t = {P}).
Exemplo:
Sejam as retas s e t com as equações gerais x + 2y – 3 = 0 e 2x + y + 2 = 0, respectivamente. Encontre o ponto P(x0, y0) comum às retas.
Resolução:
A solução para esse problema é encontrar a solução do sistema de equações formado pelas duas equações apresentadas na questão. Então, temos o sistema:
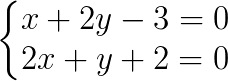
Simplificando a primeira equação na variável x, temos:
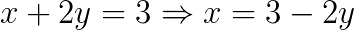
Substituindo x na segunda equação:
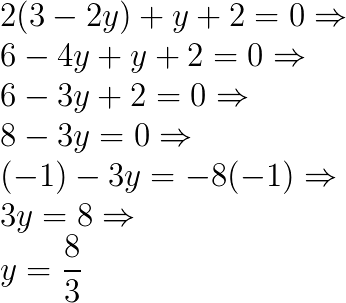
Por fim, substituindo o valor encontrado para y na primeira equação, temos:
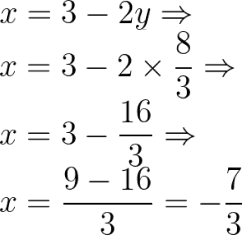
Portanto, o ponto de intersecção P(x0, y0) tem coordenadas no plano cartesiano iguais a –7/3 e 8⁄3, e P(-7/3, 8⁄3)
Exercícios
Acesse os exercícios no link abaixo:



