O triângulo escaleno é uma categoria de triângulo que possui os três lados com medidas diferentes. Além disso, as medidas dos ângulos internos do triângulo são diferentes. A soma dos ângulos internos dessa categoria de triângulo é igual a 180°.
O triângulo escaleno não é um polígono regular e não possui eixo de simetria.
Área do triângulo escaleno
Para calcular a área do triângulo escaleno usaremos nossos conhecimentos em trigonometria. Pois, no cálculo da altura (h) do triângulo, devemos calcular o produto da função seno do ângulo com um dos lados. Veja:
Exemplo:
Seja o triângulo escaleno ABC a seguir. Para calcular a altura (h) traçamos uma reta perpendicular em relação à base (b):

Dessa forma, a altura h para o triângulo é: h = c . seno(A).
Então, se substituirmos na fórmula geral para o cálculo da área de um triângulo qualquer, temos que a área é dada por:
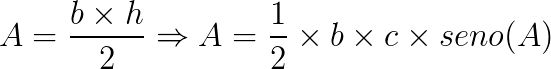
Onde:
- A: representa a área do triângulo;
- b: representa a base do triângulo, neste caso;
- c: representa um dos lados do triângulo.
Dependendo da posição do triângulo, a base pode ser outro lado do triângulo acima, dessa forma, devemos utilizar uma das fórmulas a seguir:

Perímetro do triângulo
Para calcular o perímetro do triângulo, basta utilizar a seguinte fórmula:
P = a + b + c
Onde:
- P: representa o perímetro do triângulo;
- a, b e c: representam os lados.
Lembrando que o perímetro é a soma das medidas dos lados de um triângulo.
Exercício resolvido
Seja o triângulo escaleno ABC com as seguintes medidas para os lados: 11 cm, 4 cm e 8 cm. Calcule a área e o perímetro para o triângulo.

Antes, precisamos encontrar o valor da altura h para o triângulo: h = 11 . seno(C)

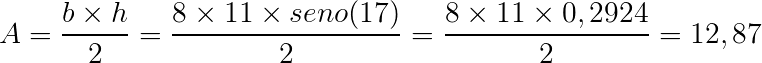
Então, a área é: 12,87 cm²
O perímetro de um triângulo é a soma de seus lados, dado pela seguinte fórmula:
P = a + b + c
Então, o perímetro para o triângulo dado é:
P = 11 + 8 + 4 = 23 cm
É isso.
Exercícios propostos
Veja os exercícios no link abaixo:



