Área e Perímetro são conceitos utilizados na Geometria. A área é usada para calcular a medida de uma superfície plana e o perímetro é usada para calcular a soma das medidas dos lados de uma figura ou objeto.
Área
A área de uma figura é a medida equivalente a sua superfície. Para calcularmos a área de uma superfície, geralmente, multiplicamos a base (b) pela altura (h) do objeto.
As unidades de medida utilizadas no cálculo da área são:
- km²: quilômetro quadrado;
- hm²: hectômetro quadrado;
- dam²: decâmetro quadrado;
- m²: metro quadrado;
- dm²: decímetro quadrado;
- cm²: centímetro quadrado;
- mm²: milímetro quadrado.
As unidades de medidas acima estão elevadas ao quadrado, ou seja, a potência de 2, pelo fato da área de uma superfície ser equivalente à divisão em “pedaços” de 1 m². Cada metro quadrado de uma área é equivalente a uma unidade de área.
Exemplo:
Para calcularmos a área de uma praça quadrada, utilizaremos o metro (m) como unidade de medida. Dessa forma, a unidade de medida é 1 m². Então, calcular a área de uma praça é o mesmo que dividi-la em vários pedaços de 1 m² e somar todos eles.

Para evitar esse desconforto, esse processo é equivalente a pegar a medida de um lado (comprimento ou base) e multiplicar por outro (largura ou altura, dependendo da posição do objeto). Veja na imagem:
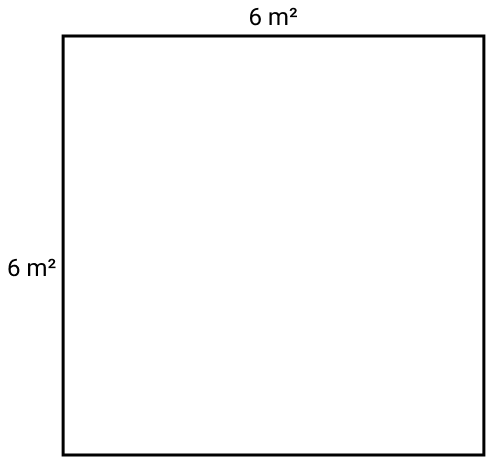
Área = 6 m² . 6 m² = 36 m²
Perímetro
O perímetro é a soma das medidas de comprimentos das bordas de uma figura.
No caso de figuras quadradas e retangulares, basta somarmos as medidas das bordas dos seus lados.
Exemplo:

Perímetro do quadrado = 6 + 6 + 6 + 6 = 24 m
Perímetro do retângulo = 4 + 16 + 4 + 16 = 40 m
Em figuras onde não é possível determinar as medidas dos lados, podemos utilizar o auxílio de um barbante.
Exemplo:

Para calcular o perímetro neste caso, basta medir o tamanho do barbante ou corda.
Em figuras onde é possível medir seus lados, mas que não são retangulares e nem quadradas, o perímetro é a soma das medidas de todos os seus lados.
Exemplo:

Perímetro = 2 + 2 + 3 + 3 + 10 + 10 = 30 cm
No cálculo do perímetro, utilizamos a unidade de medida de comprimento. Diferentemente da área, no perímetro a unidade de medida não é elevada ao quadrado.
As unidades de medida de comprimentos são:
- km: quilômetro;
- hm: hectômetro;
- dam: decâmetro;
- m: metro;
- dm: decímetro;
- cm: centímetro;
- mm: milímetro.
Área e Perímetro de Figuras Planas
Na geometria plana existem diversas figuras planas, vamos mostrar como calcular a área e o perímetro de algumas delas.
Triângulo
O triângulo é uma figura plana formada por três lados, fechada, com três ângulos internos que sua soma é igual a 180°.

Conheça mais sobre os tipos de triângulos
Retângulo
O retângulo é uma figura plana formada por quatro lados e fechada. As medidas de dois lados são iguais, da mesma forma que os outros dois lados também são iguais.

Para evitar somar todos os lados no cálculo do perímetro, neste caso multiplicamos a altura e a base por 2, pois as medidas dos lados correspondentes as estas medidas são iguais.
Quadrado
O quadrado é uma figura plana formada por quatro lados com as mesmas medidas. É fechado em todas as extremidades e possuem quatro ângulos retos (medem 90°).

No caso do perímetro do quadrado é a soma dos 4 lados que é equivalente a multiplicar um lado por 4.
Círculo
O círculo ou circunferência é uma figura plana fechada por uma linha em curva. O cálculo da área do círculo não é trivial. Devemos fazer o produto da medida do raio (uma reta do centro até a borda do círculo) ao quadrado por uma constante chamada de Pi ( π = 3,1415…).

As medidas acima são aproximadas, pois, em figuras circulares é difícil encontrar o valor de uma área ou perímetro exatos.
O perímetro da circunferência é equivalente a calcular o perímetro do círculo.
Trapézio
O trapézio é uma figura plana fechada com dois lados e bases paralelas, uma dessas bases é chamada de base maior (maior medida) e a outra de base menor (menor medida).

Losango
O losango é uma figura plana fechada com quatro lados. Os lados de um losango tem as mesmas medidas. No entanto, o losango não é equivalente a um quadrado, porque a medida dos seus ângulos não são retos. Além disso, os ângulos opostos tem medidas iguais.

Onde:
- D: medida da diagonal maior;
- d: medida da digonal menor.
Propriedades do Losango
- Os ângulos opostos são congruentes;
- As diagonais são bissetrizes;
- As diagonais são retas perpendiculares;
- Qualquer losango tem um círculo inscrito.
Exercícios
Acesse os exercícios clicando no link a seguir:



