Potenciação: Propriedades e Exemplos

Potenciação ou exponenciação é a forma de abreviar a multiplicação de uma sequência de fatores iguais.

Dessa forma, quando multiplicamos um número sucessivas vezes, podemos abreviar elevando-o a quantidade de vezes que o número é multiplicado.

Índice do Artigo

Definição de potenciação

Seja um número real a e um número natural n, com n > 1, chamamos de potência de base a e expoente n o número aⁿ, isto é, o produto de n fatores iguais a a.

Exemplo:

• a² = a.a, com n = 2;
• a³ = a.a.a, com n = 3;
• a⁵ = a.a.a.a.a, com n = 5;

Chamamos a de base e n de expoente, e a multiplicação sucessiva após a igualdade chamamos de potência.

A base nesse caso é o número que se repete, o expoente é a quantidade de vezes que esse número se repetiu e a potência é o resultado.

Potência com expoente negativo

Seja a um número real diferente de zero, e n um número natural, chamamos de potência de base a e expoente -n o número a^-n, que é o número inverso de aⁿ.

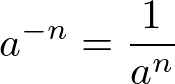
Exemplo:

Seja a multiplicação 3 x 3 x 3 x 3, temos uma sequência do número 3 multiplicado 4 vezes. Assim, podemos simplificar da seguinte forma:

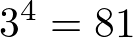
Leia-se: três elevado a quatro é igual a oitenta e um

onde, 3 é o número multiplicado e 4 a quantidade de vezes que ele foi multiplicado.

Agora com expoente negativo.

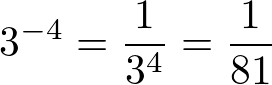
Outros tipos de potência

Expoente inteiro maior que 1.

Neste caso é o produto de vários fatores iguais à base de acordo com quantas forem as unidades do expoente.

Exemplo:

• 4³ = 4 x 4 x 4 = 64
• 5² = 5 x 5 = 25

Expoente igual a 1.

Neste caso, todas as potências com expoente 1 é igual a base. Logo:

• a¹ = a

Exemplo:

• 2¹ = 2;
• 25¹ = 25

Expoente igual a zero.

Neste caso, todas as potências com expoente igual a zero é igual a 1. Logo:

• a⁰ = 1

Exemplo:

• 3⁰ = 1
• 8⁰ = 1

Casos particulares de potenciação:

Sendo n um número inteiro, podemos ter:

• a = 0 e n > 0 ⇒ aⁿ = 0
• a = 0 e n < 0 ⇒ não existe aⁿ ∈ R
• a > 0 ⇒ aⁿ > 0
• a < 0 e n par ⇒ aⁿ > 0
• a < 0 e n ímpar ⇒ aⁿ < 0

Propriedades da potenciação

Considerando as bases a e b números reais, e os números naturais para m e n. Temos as seguintes propriedades:

Qualquer número real elevado ao expoente natural 1 é igual ao próprio número.

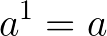
Exemplo: 5¹ = 5

Qualquer número real não-nulo elevado ao expoente natural 0 é igual a 1.

Exemplo: 3⁰ = 1

Qualquer potência que possui na base o número 1 é igual a 1.

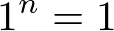
Exemplo: 1¹⁰⁰ = 1

Qualquer potência que tem na base o número 10, o resultado é o número 1 seguido da quantidade de zeros, de acordo com o valor do expoente.

Exemplo: 10⁵ = 100000

Veja que a quantidade de zeros foi definida pelo expoente 5.

Um potência com expoente negativo indica que temos uma inversão entre o numerador com o denominador.

Veja que a potência foi para o denominador sem o sinal, e o numerador é representado pelo número 1 (oculto) do denominador.

Uma potência negativa no denominador é equivalente ao numerador vezes o denominador com o sinal da potência trocado.

Exemplo:

e

No primeiro caso o 1 (um) pode ser omitido porque não altera o valor do produto, 1 x 5² = 5² = 25.

Propriedades operatórias da potenciação

É importante conhecer as propriedades operatórias para auxiliar e simplificar os cálculos envolvendo potenciação.

Produto de potências de mesma base

Ao multiplicar duas ou mais potências de mesma base, devemos proceder da seguinte forma: conservar a base e somar os expoentes.

• a^m.aⁿ = a^{m + n}

Exemplo: 5².5³ = 5^{2 + 3}

Divisão de potências de mesma base

Ao dividirmos potências não-nulas de mesma base, devemos proceder da seguinte forma: conservar a base e subtrair os expoentes.

Exemplo:

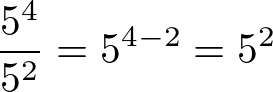
Base negativa e expoente ímpar

Quando a base é negativa e o expoente é ímpar o resultado será negativo, veja o jogo de sinais em subtração.

Exemplo: (-2)³ = -8

Base negativa e expoente par

Quando a base é negativa e o expoente é par o resultado é positivo, veja o jogo de sinais em subtração.

Exemplo: (-5)² = 25

Potência de potência

Neste caso, devemos conservar a base e multiplicar os expoentes.

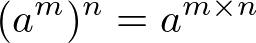
Exemplo:

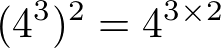
Potência de um produto

Devemos atribuir o expoente aos fatores do produto.

• (a . b)ⁿ = (aⁿ . bⁿ)
• Exemplo: (2 . 3)² = (2² . 3²) = 2 . 2 . 3 . 3 = 36

Divisão de potências de mesmo expoente

Numa divisão com expoente devemos elevar tanto o numerador quanto o denominador ao expoente.

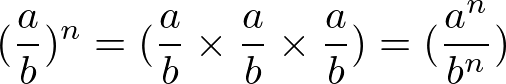
Exemplo:

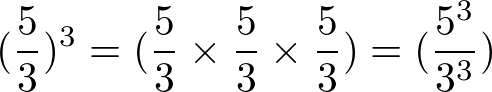
Multiplicação de potências com o mesmo expoente

Quando multiplicarmos uma potência com o mesmo expoente podemos conservar o expoente e multiplicar as bases.

• (aⁿ . bⁿ) = (a . b)ⁿ
• Exemplo: (3² . 2²) = (3 . 2)²

Observação:

As propriedades que foram apresentadas acima também servem para os expoentes m e n inteiros.

Exemplos:

2³ . 2^-2 = 2^{3 + (-2)} = 2¹

5^-3 . 2^-3 = (5 . 2)^-3 = 10^-3

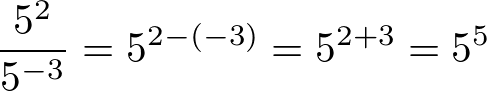
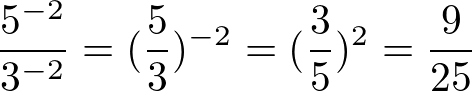
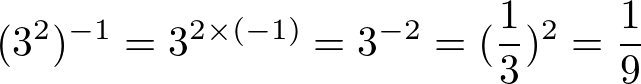
Casos especiais de potências

1. (-a)ⁿ e -aⁿ
   • Essas potências (-a)ⁿ e -aⁿ geralmente apresentam resultados diferentes, pois:
     • (-a)ⁿ = (-a) . (-a) . (-a) . … . (-a) (n vezes)
     • -aⁿ = – (a . a . a . … . a) (n vezes)
     • Exemplos:
       • (-2)² = (-2) . (-2) = 4
       • -2² = – (2 . 2) = – 4
       • (-2)³ = (-2) . (-2) . (-2) = -8
       • -2³ = – (2 . 2 . 2) = -8
     • O uso dos parênteses indica que o sinal pertence ao número e deve ser multiplicado junto.
2. (a^m)ⁿ e a^mn
   • Essas potências (a^m)ⁿ e a^mn geralmente apresentam resultados diferentes, pois:
     • (a^m)ⁿ = (a^m) . (a^m) . … . (a^m) (n vezes) e a^{m . m . … . m (n vezes)}

Exemplos:

• (5²)³ = (5²) . (5²) . (5²) = 5^2.3 = 5⁶
• 5²³ = 5^{2 . 2 . 2} = 5⁸

Potenciação é isso.

Bons estudos e boa sorte!

Veja mais…

Radiciação

Tabuada

Porcentagem

Encontrou algum erro? Nos avise clicando aqui