Unidades de medida são grandezas que compõem o sistema métrico decimal. Hoje, vamos rever algumas das unidades de medida mais importantes para resolver problemas matemáticos. Além disso, vamos mostrar as conversões e, ainda, vamos resolver alguns exercícios para facilitar o entendimento por parte do aluno.
Às vezes, ao tentar resolver um exercício torna-se necessário por parte do aluno fazer uma conversão de uma unidade de medida para outra. Vamos mostrar os símbolos de cada uma adotado por convenção no Sistema Internacional (SI).
Conheça as unidades de medida
| GRANDEZA | NOME DA UNIDADE | SÍMBOLO (SI) |
|---|---|---|
| comprimento | metro | m |
| capacidade | litro | l |
| massa | quilograma | kg |
| superfície/área | metro quadrado | m² |
| medidas agrárias | are | a |
| volume | metro cúbico | m³ |
| tempo | segundos | s |
Medidas de comprimento
Comprimento é, talvez, a medida mais utilizada no cotidiano. Por isso, acredito que todos devem ter facilidades para entender essa grandeza e sua unidade de medida.

Perceba pela imagem que para uma conversão para a direita é o mesmo que multiplicar por 10. Enquanto para a esquerda é dividir por 10.
Dessa forma, podemos entender que para multiplicar por 10 basta deslocar a vírgula para a direita uma vez, sendo a quantidade de zeros. Já para dividir basta deslocar a vírgula para a esquerda uma vez, a quantidade de zeros.
Então se quisermos converter metro (m) em milímetro (mm), multiplicamos por 1000 (10 x 10 x 10), o mesmo que deslocar a vírgula três casas à direita. Um metro tem 1000 milímetros. Se quisermos converter metros (m) em quilômetros (km), temos que dividir por 1000 (10 ÷ 10 ÷ 10), o mesmo que deslocar a vírgula três casas à esquerda. Portanto, 1 metro equivale a 0,001 km.
A unidade de medida padrão: metro (m)
- Quilômetros → 1 km = 1000 m
- Hectômetro → 1 hm = 100 m
- Decâmetro → 1 dam = 10 m
- Metro → 1 m = 1 m
- Decímetro → 1 dm = 0,1 m
- Centímetro → 1 cm = 0,01 m
- Milímetro → 1 mm = 0,001 m
Exemplos:
-
Converter 10 dam em cm:
- dam → m → dm → cm
- 10 dam = 100 m = 1.000 dm = 10.000 cm
- É o mesmo que deslocar a vírgula para a direita em três casas:
- 10 dam = 10.000 cm
-
Converter 320 dm em km:
- km ← hm ← dam ← m ← dm
- É o mesmo que deslocar a vírgula quatro casas à esquerda.
- 320 dm = 0,032 km
Medidas de capacidade
Medidas de capacidade também é muito importante no nosso cotidiano. A unidade padrão para essa grandeza é o litro (l).
- Quilolitro → 1 kl = 1000 l
- Hectolitro → 1 hl = 100 l
- Decalitro → 1 dal = 10 l
- Litro → 1 l = 1 l
- Decilitro → 1 dl = 0,1 l
- Centilitro → 1 cl = 0,01 l
- Mililitro → 1 ml = 0,001 l
Exemplo:
-
Converter 20 ml em dl
-
dl ← cl ← ml
Basta deslocar a vírgula duas casas decimais à esquerda. - 20 ml = 0,20 dl
-
Pela imagem abaixo, veja que converter é o mesmo que dividir por 10 para a esquerda ou multiplicar por 10 para a direita. Também pode se entender que essa multiplicação ou divisão é o mesmo que deslocar a vírgula uma vez de uma unidade para a outra.
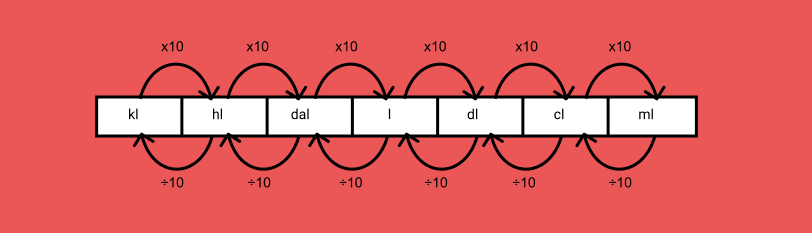
Medidas de massa
A grandeza massa não é muito usual no dia a dia, mas muito comum quando nos deparamos com problemas de física. Unidade padrão: quilograma (kg)
- Quilograma → 1 kg = 1000 g
- Hectograma → 1 hg = 100 g
- Decagrama → 1 dag = 10 g
- Grama → 1 g = 1 g
- Decigrama → 1 dg = 0,1 g
- Centigrama → 1 cg = 0,01 g
-
Miligrama → 1 mg = 0,001 g
Dizemos que 1.000 kg corresponde a 1 tonelada
- 1 t = 1.000 kg
Exemplos:
-
Converter 32 g em hg:
-
hg ← dag ← g
Deveremos deslocar a vírgula duas casas decimais para a esquerda. - 32 g = 0,32 hg
-
- Converter 782 kg em toneladas:
Uma tonelada (1t) equivale a 1.000 kg. Assim, devemos dividir a quantidade de kg por 1.000, o mesmo que deslocar a vírgula três casas decimais à esquerda.
Logo, 782 kg = 0,782t
Estude a imagem para entender melhor.
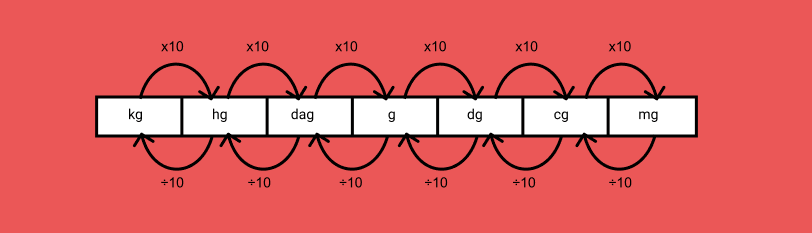
Medidas de superfície ou área
Medidas de superfície ou área também está presente no nosso dia a dia. A unidade de medida padrão é: metro quadrado (m²)
- 1 km² → 1.000.000m² = 106m²
- 1 hm² → 10.000m² = 104m²
- 1 dam² → 100m² = 102m²
- m² → 1m² = 1 m²
- 1 dm² → 0,01m² = 10-2m²
- 1 cm² → 0,0001m² = 10-4m²
- 1 mm² → 0,000001m² = 10-6m²
Medidas agrárias
Os fazendeiros devem conhecer essas unidades de medida muito bem e, aqui, você também vai entender. A unidade de medida padrão é: are (a)
- 1 a = 1 dam²
- Hectare (ha) = 1 hm² (100 m x 100 m) ou (10m x 1000m) ou (1m x 10.000m) igual a 10.000m²
-
Centiare (ca) = 1 m²
Exemplos:
-
Converter 3,2 hm² em m²:
-
hm² → dam² → m²
- 3,2 hm² = 320 dam² = 32.000
m²
É o mesmo que deslocar a vírgula quatro casas decimais à direita, pois as unidades são quadradas.
-
Converter 48,6 dm² em m²:
-
m² ← dm²
Deveremos deslocar a vírgula duas casas decimais à esquerda.
- 48,6 dm² = 0,486 m²
-
m² ← dm²
-
Converter 21,7 ha (hectare) em
km²:
- 21,7 ha = 21,7 hm²
- km² ← hm²
Deveremos deslocar a vírgula duas casas decimais à esquerda.
- 21,7 ha = 21,7 hm² = 0,217 km²
-
Medidas de volume
Quem nunca quis saber quanto cabe em uma caixa d’água, por exemplo. Para essa grandeza utilizamos a unidade de medida padrão: metro cúbico (m³)
- 1 km³ = 109 m³
- 1 hm³ = 106 m³
- 1 dam³ = 103 m³
- m³ → 1 m³ = 1 m³
- 1 dm³ = 10-3 m³ (equivale a 1 litro)
- 1 cm³ = 10-6 m³
- 1 mm³ = 10-9 m³
Exemplos:
- Converta 2.578 mm³ em dm³:
-
dm³ ← cm³ ← mm³
- 2.578 mm³ = 2,578 cm³
= 0,002578 dm³
Na prática, é o mesmo que deslocar a vírgula seis casas decimais para esquerda.
-
- Converta 28,3 m³ em dm³:
-
m³ → dm³
Deveremos deslocar a vírgula três casas decimais para a direita.
- 28,3 m³ = 28.300 dm³
-
m³ → dm³
Medidas de tempo
A unidade de medida de tempo é uma das mais importantes utilizadas na física e também no nosso dia a dia. No sistema internacional de medidas (SI), a medida de tempo é o segundo (s).
Dessa forma, em muitos casos o aluno terá que saber converter de horas para segundos, de minutos para segundos ou vice-versa.
1 hora (h) = 3600 segundos (s)
1 minuto (min) = 60 segundos (s)
1 hora (h) = 60 minutos (min)
1 dia = 24 horas (h)
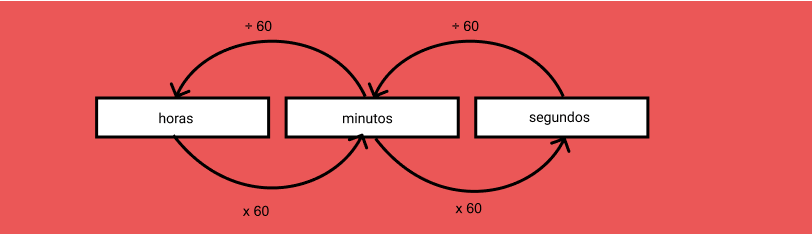
Pela imagem percebemos que para converter de horas para minutos, horas para segundos e ao contrário também, basta multiplicar ou dividir por 60.
Exemplos:
- Converter 3 horas para segundos
- 3 x 60 x 60 = 10800 segundos
- Converter 3 horas para minutos
- 3 x 60 = 180 minutos
- Converter 3600 segundas para horas
- 10800 ÷ 60 ÷ 60 = 3 horas
- Converter 180 minutos para horas
- 180 ÷ 60 = 3 horas
- Converter 10800 segundos para minutos
- 10800 ÷ 60 = 180 minutos
- Converter 180 minutos para segundos
- 180 x 60 = 10800 segundos
Legal, não é? Estas são algumas das unidades de medida mais importantes e conhecidas.
Bons estudos!
Exercício resolvido
(Agente Penitenciário SP) Dois reservatórios de água têm a mesma capacidade. O primeiro
tem a forma de um cubo, cujas arestas internas medem 2,0 metros, e o segundo tem a forma
de um paralelepípedo reto-retângulo cujas dimensões internas, em metros, são: 4,0 de
comprimento; 2,0 de largura e x de altura.
A medida x, em metros, é:
- (A) 1,00
- (B) 1,25
- (C) 0,75
- (D) 1,50
- (E) 2,50
Como os dois reservatórios tem a mesma capacidade, temos que a capacidade do cubo é a mesma do paralelepípedo ou reto-retângulo.
O cálculo da área do cubo é: largura x comprimento x altura ou simplesmente a³
Sendo que tanto o comprimento, a altura e a largura tem as mesmas mediadas.
O cálculo da área do retângulo é: base x altura, mas aqui temos um retângulo tridimensional e devemos usar a mesma fórmula do cubo, porém aqui não temos medidas iguais. Assim, será: comprimento x largura x altura.
Devemos fazer assim, pois tem as mesmas capacidades:
Cubo = paralelepípedo (reto-retângulo)
2³ = 4 * 2 * x
Agora só resolver: 2³ é 2 x 2 x 2 = 8
8 = 8x ⇒ x = 8⁄8 = 1 ⇒ x = 1
1 metro (m)
Logo, alternativa A.



