Dizemos que duas retas são perpendiculares se elas se cruzam num ponto comum entre si e formam um ângulo de 90°. Esse ângulo é chamado de ângulo reto.
Para representarmos que duas retas r e s são perpendiculares entre si, utilizamos o símbolo ⊥. Assim: r ⊥ s.
As retas perpendiculares são um caso particular das retas concorrentes.
Perpendicularidade entre duas Retas
Para que duas retas sejam perpendiculares entre si, é necessário que elas sejam concorrentes. Além disso, o ângulo formado deve ser de 90°.
Dessa forma, seja r uma reta com coeficiente angular m1 e uma reta s com coeficiente angular m2.
As r e s serão perpendiculares entre si se formarem 4 (quatro) ângulos de 90°, então r ⊥ s se, e somente se,
- m1 . m2 = -1 ou
- m2 = – 1/m1 ou
- m1 = – 1/m2.
Portanto, se duas retas são perpendiculares entre si, então o coeficiente angular de uma é o oposto do inverso do coeficiente angular da outra, e vice-versa.
Exemplo:
Seja as retas r e s no plano cartesiano e perpendiculares no ponto P.
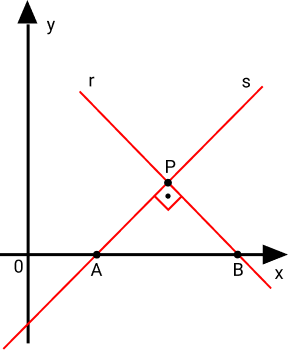
Seja o ângulo de inclinação de s representado por β, assim o ângulo de inclinação de r deverá ser 90° + β. Com isso, temos:
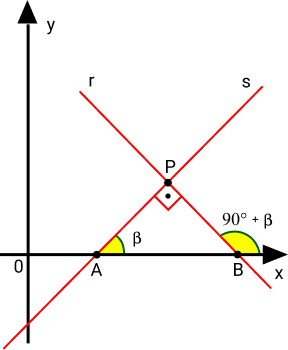
- Coeficiente angular de s: ms = tan(β)
- Coeficiente angular de r: mr = tan(90° + β)
Sabendo que ms = tan(β) e mr = – 1/tan(β). Então:
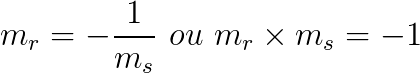
Podemos demonstrar isso aplicando as relações sobre a soma de arcos:
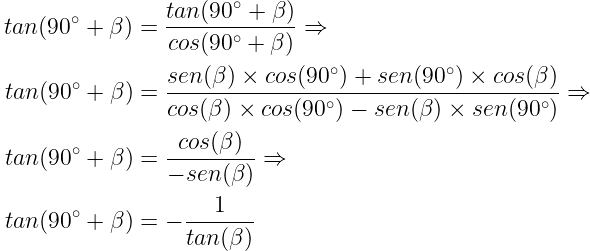
Portanto, podemos concluir que o coeficiente angular de r é:
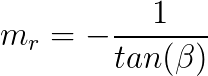
Logo:
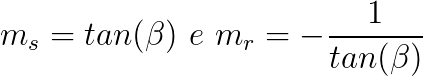
Concluímos que as retas r e s são perpendiculares entre si, pois o coeficiente angular de r é igual ao oposto do inverso do coeficiente angular de s.
Como saber se duas retas são perpendiculares entre si?
Existe um método prático para sabermos se duas retas são perpendiculares entre si. Para isso é necessário que conheçamos a equação geral das duas retas. Através da equação podemos verificar a perpendicularidade usando os coeficientes x e y.
Portanto, se duas r e s tem equação igual a ar x + bry + cr = 0 e asx + bsy + cs = 0, respectivamente. Então, podemos verificar se r e s são perpendiculares fazendo:
ar . as + br . bs = 0
Assim, se a soma do produto acima for 0 (zero), então r e s são perpendiculares.
Retas Perpendiculares no Plano
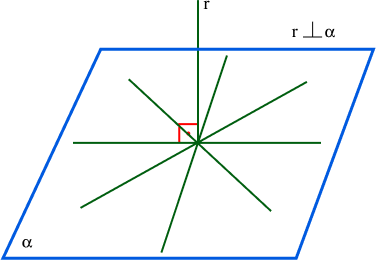
Uma reta r é perpendicular a um plano α, se r forma um ângulo reto (90°) a duas retas concorrentes no plano α. Generalizando, uma reta r é perpendicular a um plano α se r for perpendicular a todas as retas contidas no plano.
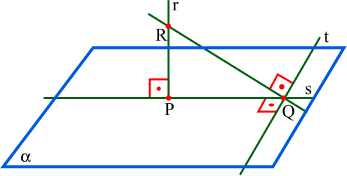
Teorema das três perpendiculares entre as retas
Seja r uma reta perpendicular a um plano α em um ponto qualquer P no plano. Seja s outra reta contida em α e passando por P. Seja t outra reta contida em α, mas que não passa por P e perpendicular a s em outro ponto Q no plano α. Seja R um ponto qualquer de r. Então, podemos dizer que a reta RQ é perpendicular à reta t.
Propriedades da Perpendicularidade de uma Reta com o Plano
Se duas retas são perpendiculares num mesmo plano, então elas são paralelas: r ⊥
α e s ⊥ α ⇔ r // s;
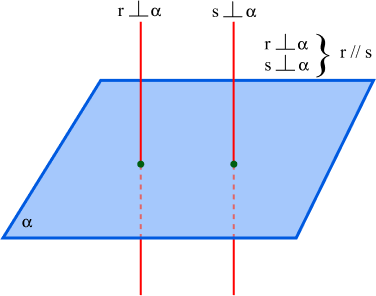
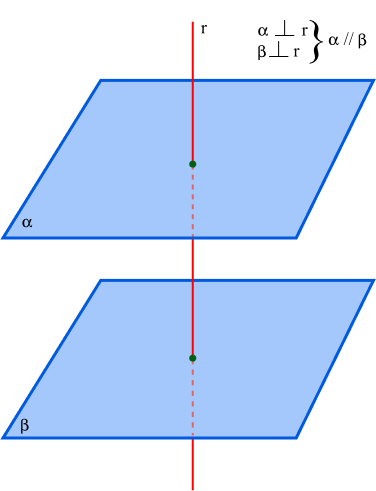
Se dois planos são perpendiculares a uma mesma reta, então eles são paralelos: α
⊥ r e β ⊥ r ⇔ α // β;
Exercício Resolvido
Determine a equação da reta r, sabendo que s é perpendicular à reta r, e s tem equação 3x + 2y – 2 = 0 e passa pelo ponto P(1, 2).
Resolução:
Vamos encontrar o coeficiente angular de s:
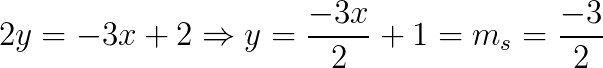
Sabemos que r é perpendicular a s, então:
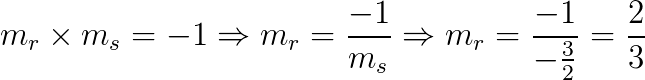
Encontramos um ponto da reta r e o seu coeficiente angular. Então, a equação de s é:
y – y0 = mr . (x – x0)
Sendo que x0 e y0 são dados pelo ponto P da questão.
Portanto,
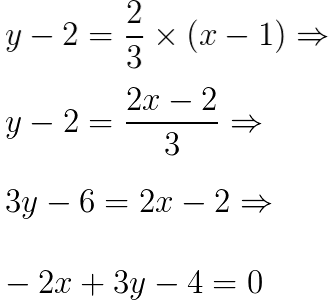
Logo a equação de r é: – 2x + 3y – 4 = 0
Exercícios propostos
Acesse e veja os exercícios propostos e resolvidos no link a seguir:



