As retas são linhas formadas por pontos e sem espaços entre eles. Elas são infinitas e ilimitadas. Dessa forma, devem possuir setas para os dois lados indicando que possuem comprimento infinito.
Para indicar os pontos da reta, devemos utilizar letras maiúsculas. Além disso, apesar de uma reta possuir infinitos pontos, só serão preciso indicar dois pontos quando desenharmos uma reta, segundo a Geometria.
É importante lembrar que as elas não fazem curvas. Quando utilizadas na geometria plana, são chamadas retas no plano, quando utilizadas na geometria espacial, são chamadas retas no espaço.
Exemplo:

É importante informar, como visto na imagem acima, que as elas podem estar dispostas no plano na horizontal, vertical ou inclinada.
Elementos das Retas
As retas não possuem definição na matemática, no entanto, podemos dizer que uma reta é uma figura geométrica unidimensional, ou seja, só possui uma dimensão.
Só podemos medir o comprimento dos objetos na reta. Esses objetos são:
Semirreta
Uma semirreta é definida por dois pontos A e B, onde A é o ponto de origem e B um ponto qualquer. O ponto A, que indica a origem da semirreta, corta a reta de modo que apenas um lado seja infinito. Então, uma semirreta é uma parte da reta, infinita somente de um lado.
Exemplo:

Segmento de Reta
O segmento de reta é outro objeto que podemos destacar numa reta. O segmento de reta é formado por dois pontos A e B, o espaço entre A e B é o que chamamos segmento de reta. Dessa forma, diferentemente das semirretas, os segmentos de reta são finitos.
Exemplo:

Classificação das Retas
Podemos classificá-las de acordo com seu tipo e disposição no plano.
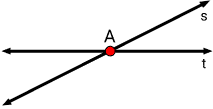
Concorrentes
São chamadas concorrentes quando elas possuem um único ponto em comum, sendo onde elas se cruzam. Um caso particular de retas concorrentes são as perpendiculares.
Exemplo:
Paralelas
São retas que não se encontram e assim não possuem pontos nem ângulos em qualquer parte das retas. Elas são posicionadas lado a lado em qualquer sentido.
Exemplo:

Para dizer que uma reta é paralela a outra, fazemos: s // t
Coincidentes
São retas em que dois ou mais pontos de uma reta coincidem com outra. Dessa forma, na geometria, duas retas coincidentes são uma só.
Exemplo:

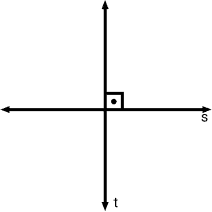
Perpendiculares
São perpendiculares entre si quando as retas se cruzam em um ponto e formam um ângulo reto (ângulo de 90°).
Exemplo:
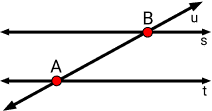
Transversais
Uma reta é chamada transversal quando ela se cruza com outras duas retas em pontos diferentes.
Exemplo:
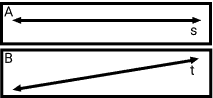
Coplanares
São chamadas de coplanares quando elas pertencem ao mesmo plano, na imagem ao plano B.
Exemplo:

Reversas
São chamadas reversas quando elas pertencem a planos diferentes.
Exemplo:
Propriedades
- As retas são infinitas;
- São unidimensionais, ou seja, possui apenas uma dimensão;
- O conjunto dos pontos são infinitos;
- No plano, elas podem ser dispostas na horizontal, vertical e de forma inclinada.
Equação Geral da Reta
Uma reta representada no plano cartesiano possui uma equação, chamada equação geral da reta, e pode ser escrita da seguinte forma:
ax + by + c = 0
Onde:
- a, b e c: são conhecidos e constantes, com a ≠ 0 ou b ≠ 0;
- x e y: são as coordenadas do plano cartesiano em um ponto P qualquer, P(x, y).
Equação Reduzida da Reta
Uma reta quando representada no plano cartesiano que passa pelo ponto P(0, n), com coeficiente angular m, possui uma equação, chamada equação reduzida da reta, e pode ser escrita da seguinte forma:
y = mx + n
Onde:
- x e y: são as coordenadas do plano cartesiano;
- m: é o coeficiente angular;
- n: é o coeficiente linear.
Exercícios
Veja os exercícios acessando o link abaixo:



