Um segmento de reta é uma parte da reta que possui início e fim, ou seja, dois pontos A e B, onde A é a origem e B é o final do segmento.
Os segmentos de retas são finitos. Na sua representação na matemática utilizam-se colchetes, que indicam um intervalo fechado com um traço acima das letras indicando segmento de reta. Os colchetes são facultativos.
Exemplo:
Considere a reta r abaixo:

A parte em vermelho delimitada pelos pontos A e B é o que chamamos de segmento de reta. Os segmentos de retas podem aparecer também nas semirretas.
A diferença entre reta, semirreta e segmento de reta, é as retas são infinitas para ambos os lados, as semirretas são infinitas somente em um sentido. Já os segmentos de retas são finitos. Eles são limitados por dois pontos em uma reta, que são os extremos do segmento.
Tipos de Segmentos de Retas
Podemos ser classificá-los de acordo com sua disposição no plano. Vamos ver todos os tipos a seguir:
Segmentos Consecutivos:
São os segmentos que possuem um ponto em comum, ou seja, dois ou mais segmentos possuem um ponto comum que é compartilhado entre eles. Veja na imagem a seguir:
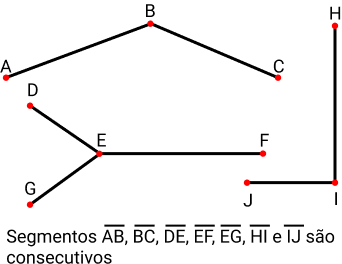
Os segmentos [AB] e [BC] compartilham o ponto B. Os segmentos [DE], [EF] e [EG] compartilham o ponto E. Os segmentos [HI] e [IJ] compartilham o ponto I.
Segmentos Colineares:
São chamados de colineares quando eles compartilham a mesma reta, ou seja, pertencem a mesma reta ou passa pela mesma reta. Veja:

Segmentos Adjacentes:
São chamados de ajacentes quando eles são, ao mesmo tempo, consecutivos e colineares. Esse tipo de segmento pode possuir um ou mais pontos em comum e deve, necessariamente, pertencer a mesma reta. Veja um exemplo na imagem:
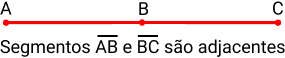
Segmentos Congruentes:
Dois ou mais segmentos de retas são chamados de congruentes quando eles possuem as mesmas medidas. Veja:

É importante lembrar que dois segmentos de retas paralelas podem ser congruentes. Mas não serão consecutivos, colineares e nem adjacentes.
Ponto Médio do Segmento
Quando temos um segmento de reta e entre eles um ponto qualquer, esse ponto é o ponto médio do segmento se ele dividir o segmento exatamente ao meio. Dessa forma, o ponto médio forma dois segmentos simétricos.
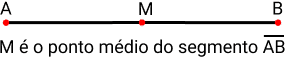
Na imagem, M é o ponto médio se os segmentos AM e MB forem congruentes, ou seja, se tiver a mesma medida. Sendo assim, M divide o segmento AB exatamente ao meio.
Em um triângulo retângulo, o segmento de reta AB, que representa a hipotenusa, tem como ponto médio M se M divide o segmento AB na metade.
Exemplo:
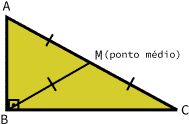
Isso pode ser demonstrado se pegarmos o triângulo retângulo acima, transformá-lo em dois, unirmos as hipotenusas formando um retângulo. O ponto M, que divide a hipotenusa na metade, ficará no centro do retângulo.
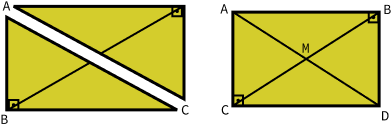
Assim, M é o ponto médio da hipotenusa do triângulo ABC. Então, se AD = BC e AM = AD/2, logo AM = BC/2



