Responda os exercícios abaixo para treinar os conhecimentos sobre retas perpendiculares.
1) Determine a equação da reta r que passa pelo ponto A(2, 1), sendo r perpendicular à reta s: 3x + 2y – 1 = 0.
Ver resposta
Isolando y na reta s e encontrando o coeficiente angular, temos:
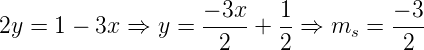
Sabendo que s é perpendicular r, então:
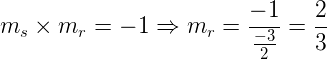
A partir do ponto A(2, 1) e do coeficiente angular de r podemos encontrar a equação da reta r, fazendo:
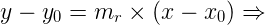
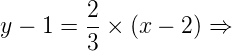
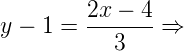
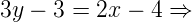
3y – 3 – 2x + 4 = 0 ⇒
– 2x + 3y + 1 = 0
Portanto, essa é a equação da reta r perpendicular a s.
2) Prove que as retas da questão 1 são perpendiculares.
Ver resposta
Equação da reta s: 3x + 2y – 1 = 0
Coeficiente angular de s:
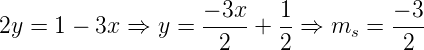
Equação da reta r: – 2x + 3y + 1 = 0
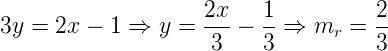
r e s são perpendiculares de mr . ms = – 1
Assim,
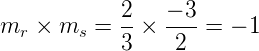
Portanto, r e s são perpendiculares.
3) Determine o valor de k para que a reta r: kx – y – 8 = 0 seja perpendicular a reta s: 3x + 2y – 3 = 0.
Ver resposta
Sabemos que duas retas são perpendiculares quando o produto entre seus coeficientes angulares seja igual a -1.
r: kx – y – 8 = 0 ⇒
– y = – kx + 8 ⇒
y = kx – 8 ⇒ mr = k
s: 3x + 2y -3 = 0 ⇒
2y = – 3x + 3 ⇒
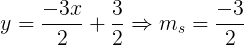
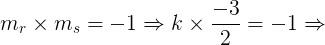
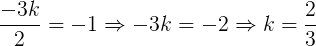
Portanto, o valor de k = 2/3 para que r e s sejam perpendiculares.
Exercícios simples para você entender um pouco mais sobre retas perpendiculares.


