O quadrado é um quadrilátero (quatro lados) regular com lados congruentes (mesma medida) e ângulos internos retos (90°). A soma dos ângulos internos é igual a 360°.

É um polígono e um quadrilátero pelo fato de ter quatro lados. Além disso, é também um paralelogramo, pois possuem lados opostos paralelos e congruentes. Todo paralelogramo possui lados e ângulos congruentes, e as diagonais se interceptam no ponto médio.
É também um tipo especial de retângulo. Além disso, um quadrado é também um losango, pois possui lados e ângulos com as mesmas medidas.
Mas, nem todo losango é um quadrado, pois os losangos que não possuem ângulos retos não são quadrados.
Definição
Uma figura geométrica é um quadrado se, e somente se, possui quatro lados e ângulos congruentes. Logo:
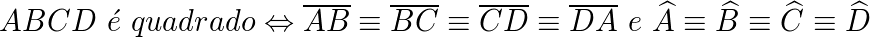
Elementos do Quadrado
É formado pelos seguintes elementos:
- Lados: os lados são segmentos de retas que se encontram nos vértices. Os lados opostos são paralelos.
- Ângulos: os ângulos medem 90° e são chamados de ângulos retos;
- Vértices: os vértices são pontos onde os lados se encontram, se ligam;
- Diagonais: as diagonais são segmentos de retas que ligam os vértices opostos, cortando-o ao meio.
Área do Quadrado
Para calcular a área temos que usar a fórmula da área para polígonos regulares de quatro lados.
A = b . h
Onde:
- A: é a área;
- b: é a medida da base;
- h: é a medida da altura.
Como o quadrado possui lados com medidas congruentes, então substituindo na fórmula teremos:
A = L . L
Assim, a fórmula para calcular a área é:
A = L²
Onde:
- A: é a área;
- L: a medida de um lado.
Perímetro do Quadrado
O perímetro é equivalente a somar todas as medidas dos lados. Assim, o perímetro é calculado pela seguinte fórmula:
P = L + L + L + L
Como possui lados com medidas iguais podemos simplificar a fórmula acima para:
P = 4 . L
Onde:
- P: é o perímetro;
- L: a medida de um lado.
Diagonal
A diagonal divide-o em dois triângulos retângulos. Assim, como se trata de um triângulo retângulo podemos aplicar o Teorema de Pitágoras para obter a medida da diagonal.

Os lados do quadrado são os catetos nos triângulos, a hipotenusa é a diagonal, e sua medida é:
- d² = L² + L² ⇒
- d² = 2 . L² ⇒
- √d² = √(2 . L²) ⇒
- d = L . √2
Propriedades
Todo quadrado apresenta as seguintes propriedades:
- As diagonais são maiores √2 vezes que a medida dos lados, assim: d = L . √2;
- As medidas dos lados são iguais ao diâmetro de uma circunferência inscrita no quadrado;
- As diagonais são perpendiculares entre si, assim todo quadrado é também um losango. Além disso, a diagonal divide os ângulos internos na metade e se cruzam no centro do quadrado.
Bons estudos!
Exercícios
Acesse os exercícios no link a seguir:



