A área do losango é a medida equivalente a superfície desse polígono. O losango é um polígono formado por quatro lados congruentes (mesma medida). Então, o losango é um quadrilátero.
O losango é também um paralelogramo, pois seus lados opostos são paralelos. Além disso, um losango com ângulos internos retos (90°) é também um quadrado. Assim como os ângulos opostos são congruentes.
Índice do Artigo
Elementos do Losango
Um losango possui os seguintes elementos:
- Lados: possui quatro lados congruentes, e os lados opostos são paralelos. Os lados são formados por segmentos de retas, também chamados de arestas, que se encontram nos vértices;
- Vértices: possui quatro vértices, os vértices são pontos onde os lados se encontram;
- Ângulos: o losango tem quatro ângulos, os ângulos opostos são congruentes. Dois ângulos são agudos (menores que 90°) e dois são obtusos (maiores que 90°). Os losangos com ângulos de 90° é conhecido como quadrado;
- Diagonais: todo losango, assim como os paralelogramos, possui duas diagonais. As diagonais se interceptam em seus respectivos pontos médios.
Como Calcular a Área de um Losango?
Para calcularmos a área de um losango devemos realizar o produto entre as medidas das diagonais e dividir por dois.
Ao traçarmos as diagonais, quatro triângulos retângulos são formados. Então, a área é igual a área dos quatros triângulos.
Fórmula da Área do Losango
Com a medida das diagonais em mãos, podemos calcular a área através da fórmula:
Onde:
- A: é a área do losango;
- D1: é a medida da diagonal 1;
- D1: é a medida da diagonal 2.
Diagonais do Losango
As diagonais do losango possuem tamanhos diferentes. Elas se cruzam nos seus respectivos pontos médios perpendicularmente e formam um ângulo reto (ângulo de 90°).
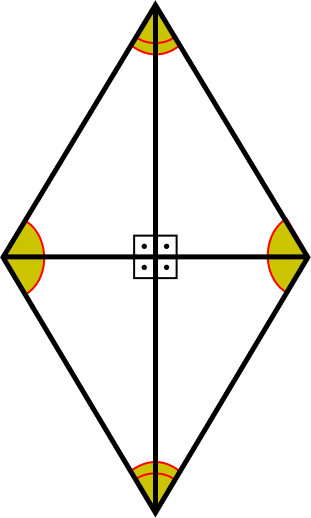
Cada diagonal divide o losango em dois triângulos congruentes. E as duas diagonais dividem o losango em quatro triângulos retângulos.
A partir da área do triângulo é que chegamos na fórmula da área do losango.
A área do triângulo é:
- A = (b . h)/2.
Onde:
- A: é a área;
- b: é a base;
- h: é a altura;
Substituindo a medida da base (b) na fórmula do triângulo pela medida da diagonal menor (d). E a altura (h) pela medida da metade da diagonal maior (D/2), chegaremos a fórmula da área do losango. Veja:
Assim,
- AL = AABC + ABCD.
Portanto, temos que:
Propriedades do Losango
Os losangos possuem as seguintes propriedades:
- Os ângulos opostos são congruentes;
- As diagonais são bissetrizes;
- As diagonais são segmentos de retes perpendiculares entre si;
- Qualquer losango tem uma circunferência inscrita.
Exercícios
Acesse os exercícios no link a seguir:
Encontrou algum erro? Avise-nos clicando aqui
by