Trapézio: Definição, Fórmula da Área e Propriedades

O trapézio é uma figura geométrica plana com dois lados paralelos entre si. Esses lados são chamados bases, o lado menor é a base menor e o lado maior é chamado base maior.

É também um quadrilátero, pois possui quatro lados, como outras figuras da geometria plana. A soma dos ângulos internos do trapézio corresponde a 360°.

Definição

O trapézio é um quadrilátero plano convexo, pois possui lados paralelos. Assim:

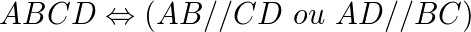
Tipos de Trapézio

Podemos classificar os trapézios de acordo com sua forma disposta no plano da seguinte forma:

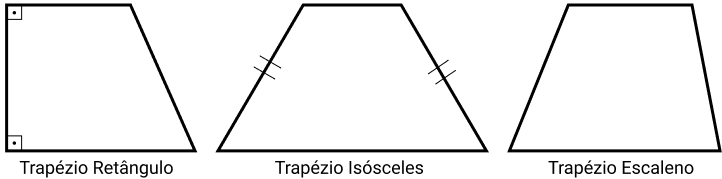
• Retângulo: possui um lado perpendicular às duas bases e formam dois ângulos retos (90°) com elas;
• Isósceles: possui dois lados com a mesma medida e as bases com medidas diferentes;
• Escaleno: possui todos os lados com medidas diferentes.

Exemplo:

Fórmula para Calcular a Área

Para calcular a área precisamos realizar o produto entre a soma das bases pela altura e dividir o resultado por dois. Dessa forma, o cálculo da área é feito com a seguinte fórmula:

Onde:

• A: é a área;
• B: é a medida da base maior;
• b: é a medida da base menor;
• h: é a altura.

Cálculo do Perímetro

O perímetro é calculado somando as medidas de todos os lados. Para isso, usamos a seguinte fórmula:

P = B + b + L₁ + L₂

Onde:

• P: é o perímetro;
• B: é a medida da base maior;
• b: é a medida da base menor;
• L₁ e L₂: são os lados.

Mediana

Se traçarmos um segmento de reta paralelo às duas bases do trapézio, dividimo-lo em dois.

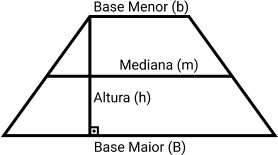
Esse segmento de reta é chamado mediana do trapézio e pode ser calculado pela seguinte fórmula:

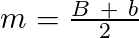
Este segmento de reta, dividindo o trapézio ao meio, é a mediana. Para calcular a área de um dos trapézios pode ser usada a seguinte fórmula:

A = m . h

Onde:

• A: é a área;
• m: é a medida da mediana, a base média;
• h: é a altura equivalente.

Podemos, ainda, calcular a medida de um dos lados usando a seguinte fórmula:

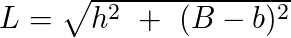
Onde:

• L: é a medida do lado;
• B: é a base maior;
• b: é a base menor;
• h: é a altura.

É importante afirmar que esta fórmula somente pode ser utilizada para calcular a medida dos lados de um trapézio retângulo.

Para calcular a medida do lado de um trapézio isósceles, substitua (B – b) por [(B – b)/2]. Assim, temos a seguinte fórmula:

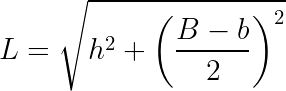
As fórmulas acima não servem para calcular a medida do lado do trapézio escaleno.

Propriedades

Temos as seguintes propriedades para essa figura geométrica:

• Todo trapézio ABCD de bases

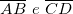
Temos que a soma dos ângulos correspondentes é igual a 360°:

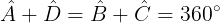
• Os ângulos das bases de um trapézio isósceles são congruentes;
• Os trapézios isósceles possuem diagonais congruentes.

Exercícios

Veja os exercícios acessando o link a seguir:

• Exercícios sobre trapézio