A Média, Moda e a Mediana são medidas de tendências centrais em um conjunto de dados numéricos utilizadas na estatística.
O objetivo destes tipos de medidas é resumir um conjunto de dados em um único número que representa um dado do conjunto.
Média Aritmética
A média de um conjunto de dados (elementos) é a razão entre a soma de todos os elementos deste conjunto e o total de elementos.
Em estatística para simbolizar a média é usado o número x com um traço em cima.
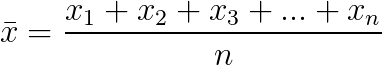
Onde:
- n é o total de números somados.
A média também pode ser simbolizada pelo somatório:

O somatório indica apenas uma soma sucessivas de vários valores, não se assuste com ele.
Como Calcular a Média?
A média é calculada utilizando a seguinte fórmula:
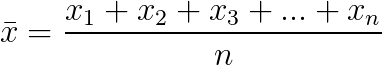
Onde:
- n é o número total de elementos
Exemplo:
Considere o conjunto de dados:
A = {2, 4, 12, 54, 3}
Assim, a média para o conjunto acima é:
(2 + 4 + 12 + 54 + 3)/5 = 15
A média pode nem sempre representar o conjunto de dados, pois, em alguns casos, em que os elementos estejam distribuídos de forma não uniforme, podemos ter uma situação atípica.
Exemplo:
Seja o conjunto de dados referente as idades de 6 pessoas:
A = {2, 3, 5, 7, 2, 90}
Esse é um conjunto de dados em que 5 pessoas são crianças e um adulto (idoso).
Assim, a média de idade é: (2 + 3 + 5 + 7 + 2 + 90)/6 = 18,17
Então, calculando a média de idade do conjunto, encontramos uma média de idade de 18 anos, porém a grande maioria das pessoas do conjunto é de crianças. 18 anos é idade de um adolescente.
Moda
A Moda (Mo) é o valor que aparece com mais frequência em um conjunto de dados, ou seja, o valor que aparece mais vezes.
Como Calcular a Moda?
Para calcular a moda de um conjunto de dados só é preciso observar os dados que aparecem com maior frequência no conjunto.
Exemplos:
Considere o conjunto de dados abaixo:
A = {2, 23, 4, 2, 5}
A moda para esse conjunto é: Mo = 2. É o número que aparece o maior número de vezes.
B = {17, 21, 2, 21, 8, 2}
Neste exemplo, a moda é: Mo = 2 ou 21. Então, podemos dizer que o conjunto B é bimodal (possui duas modas).
Mediana
A Mediana (Md) é o valor de centro de um conjunto de dados. Para calcular, primeiro devemos ordenar o conjunto de dados.
Para calcular a mediana:
- Devemos ordenar o conjunto de dados em ordem crescente;
- Se o número de elementos for par, então a mediana é a média dos dois valores centrais. Soma os dois valores centrais e divide o resultado por 2: (a + b)/2.
- Se o número de elementos for ímpar, então a mediana é o valor central.
Exemplo:
Sejam os conjuntos de dados a seguir:
- A = {3, 1, 8}
- B = {6, 4, 7, 2}
- C = {6, 7, 2, 1, 8}
Vamos seguir os passos para calcular a mediana para o conjunto A:
- Ordenar o conjunto: A = {1, 3, 8}
- O número de elementos é ímpar, então a mediana é o valor central: Md = 3
Vamos, agora, calcular a mediana para o conjunto B:
- Ordenar o conjunto: B = {2, 4, 6, 7}
- O número de elementos é par, então a mediana são os dois valores centrais dividido por 2: Md = (4 + 6)/2 = 5
Por fim, vamos calcular a mediana do conjunto C:
- Ordenar o conjunto: C = {1, 2, 6, 7, 8}
- O número de elementos é ímpar, então: Md = 6
Exercício Resolvido
(UFJF-MG: adaptado) A tabela a seguir mostra as notas de 24 alunos em um prova de Física aplicada, com nota máxima de 100 pontos.
| 40 | 20 | 10 | 20 | 70 | 60 |
| 90 | 80 | 30 | 50 | 50 | 70 |
| 50 | 20 | 50 | 50 | 10 | 40 |
| 30 | 20 | 60 | 60 | 10 | 20 |
Para a tabela com as notas acima, calcule:
- A média das notas;
- A frequência relativa da moda;
- A mediana das notas apresentadas.
Resolução:
| Notas | Frequência |
|---|---|
| 90 | 1 |
| 80 | 1 |
| 70 | 2 |
| 60 | 3 |
| 50 | 5 |
| 40 | 2 |
| 30 | 2 |
| 20 | 5 |
| 10 | 3 |
A média das notas é: 90 + 80 + (70 x 2) + (60 x 3) + (50 x 5) + (40 x 2) + (30 x 2) + (20 x 5) + (10 x 3 ) / 24 = 42,1
A moda é: Mo = 50 ou 20
A frequência relativa da moda é: 5⁄24 = 0,21 = 21⁄100 = 21%
24 é o somatório das frequências e 5 a frequência da nota que mais aparece na tabela.
Para calcular a mediana temos que organizar as notas em ordem crescente:
(10, 10, 10, 20, 20, 20, 20, 20, 30, 30, 40, 40, 50, 50, 50, 50, 50, 60, 60, 60, 70, 70, 80, 90)
Como o conjunto de elementos é formado por um número par de elementos, então a mediana é soma dos dois valores centrais dividido por 2.
A mediana é: Md = (40 + 50) / 2 = 45
Exercícios propostos
Acesse os exercícios no link a seguir:
Leis também…



