Média aritmética é a soma de vários valores e dividido pelo total deles. Ou seja, o resultado dessa divisão equivale a um valor médio entre todos os valores.
Definição de Média Aritmética
Seja os números reais x1, x2, … , xn a média aritmética é definida por:
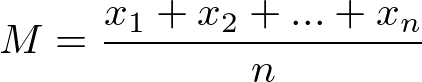
Onde n é o total de valores somados.
Exemplos
Suponha que em uma sala de aula tem 5 alunos, com as seguintes idades: 14, 12, 15, 18 e 16. Qual a idade média dos alunos dessa sala?
Dessa forma, basta somarmos todas as idades e dividir pelo total de alunos.
Logo:
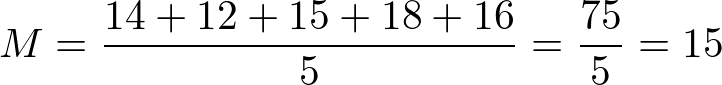
Assim, essa sala tem uma média de idade dos alunos de 15 anos.
Calcule a média entre 5, 10, 20, 100 e 200:
Basta somarmos e dividir pelo total:
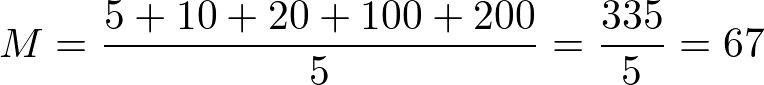
Um time de futebol fez 5 partidas em um campeonato, marcando 2 gols na primeira partida, 1 gol na segunda partida, 4 na terceira, 1 na quarta e 5 na quinta. Qual foi a média de gols por partida marcados por esse time?
Para sabermos a média aritmética de gols marcados, basta somar o total de gols e dividir pelo número de partidas.
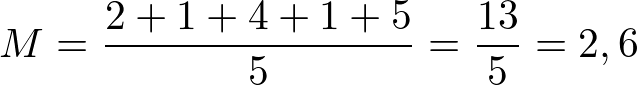
Assim, o time marcou uma média de 2,6 gols por partida.
Exercícios de vestibulares resolvidos
(PUC-SP) O histograma a seguir apresenta a distribuição de frequências das faixas salariais numa pequena empresa.

Com os dados disponíveis, pode-se concluir que a média
desses salários é,
aproximadamente,
- A) R$ 420,00
- B) R$ 536,00
- C) R$ 562,00
- D) R$ 640,00
- E) R$ 708,00
Resolução:
Analisando o histograma, precisamos encontrar o ponto médio das faixas salariais. O ponto médio de uma reta é dado pela soma de dois pontos divididos por 2, isto é, (x1 + x2)/2.
Assim, temos os seguintes pontos médios:
- Para as 14 pessoas que recebem R$ 500,00, o ponto médio é: (0 + 500)/2 = 250.
- Para as 4 pessoas que recebem R$ 1.000,00, o ponto médio é: (500 + 1000)/2 = 750.
- Para as 2 pessoas que recebem R$ 1.500,00, o ponto médio é: (1000 + 1500)/2 = 1250.
- Para as 2 pessoas que recebem R$ 2.000,00, o ponto médio é: (1500 + 2000)/2 = 1750.
- Para as 2 pessoas que recebem R$ 2.500,00, o ponto médio é: (2000 + 2500) = 2250.
Agora que encontramos o ponto médio das faixas salariais, devemos multiplicar os respectivos pontos médios pelo total de pessoas que estão naquela faixa salarial, somarmos o resultado do produto e depois dividir pelo total que são 24 pessoas.
Logo:
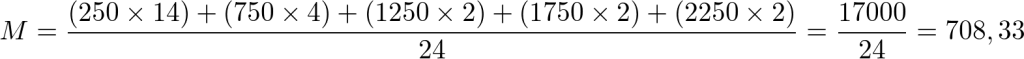
Portanto, os funcionários da empresa recebem uma média salarial de aproximadamente R$ 708,33. Então, a alternativa correta é a letra E.
(FGV-SP) A tabela a seguir apresenta a distribuição de frequências dos salários de um grupo de 50 empregados de uma empresa, num certo mês.
| Número da classe | Salário do mês em reais | Número de empregados |
|---|---|---|
| 1 | [1 000, 2 000[ | 20 |
| 2 | [2 000, 3 000[ | 18 |
| 3 | [3 000, 4 000[ | 9 |
| 4 | [4 000, 5 000] | 3 |
O salário médio desses empregados, nesse mês, foi de
- A) R$ 2.637,00
- B) R$ 2.520,00
- C) R$ 2.500,00
- D) R$ 2.420,00
- E) R$ 2.400,00
Pela tabela dada acima, temos uma faixa salarial para cada classe. Vamos calcular, primeiramente, a média salarial de cada classe:
- Classe 1: (1000 + 2000)/2 = 1500
- Classe 2: (2000 + 3000)/2 = 2500
- Classe 3: (3000 + 4000)/2 = 3500
- Classe 4: (4000 + 5000)/2 = 4500
Agora que temos a média salarial de cada classe, podemos calcular a média salarial dos empregados da empresa. Para isso, devemos multiplicar a média salarial de cada classe pelo total de empregados da classe.
Logo:
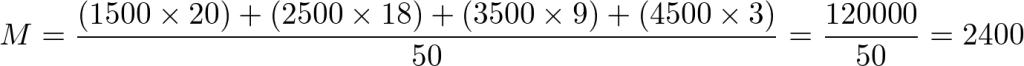
Portanto, a média salarial dos empregados da empresa é de R$ 2.400. A alternativa correta é a letra E.
Exercícios Propostos
Veja os exercícios no link a seguir:
Veja mais…



