A média ponderada consiste em multiplicar um peso em cada valor somado. Na média aritmética simples o peso para todos os valores é 1.
Sabe-se que na multiplicação qualquer valor multiplicado por 1 não tem efeito. Sendo um número neutro. Por esse motivo que não se fala em peso na média aritmética simples.
Índice do Artigo
Definição de média ponderada
Seja x1, x2, x3, … , xn números reais positivos, com p1, p2, p3, …, pn números positivos, a média ponderada é definida por:
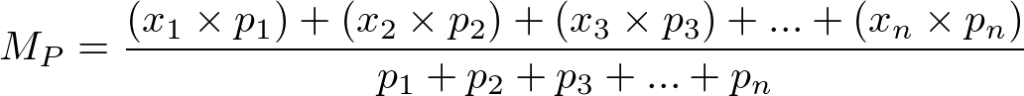
Ou seja, a média ponderada é a soma do produto de cada valor pelo seu respectivo peso e dividido pelas soma dos pesos.
Exemplo com média ponderada
A melhor forma de entender é mostrar um exemplo de como funciona.
Um professor resolveu aplicar um peso em todas as provas de uma disciplina durante o ano letivo. Foram realizadas 4 provas durante o período e os pesos em cada prova foram assim distribuídos:
- Prova 1: peso 2
- Prova 2: peso 2
- Prova 3: peso 3
- Prova 4: peso 3
João tirou na prova 1, nota 5, na prova 2, nota 7, na prova 3, nota 6 e na prova 4 deu uma relaxada e tirou nota 3. Ele foi aprovado?
Dessa forma, basta multiplicar cada nota tirada nas provas por João e multiplicar pelo peso definido pelo professor em cada prova. Somar tudo e dividir pela soma total dos pesos. Veja!
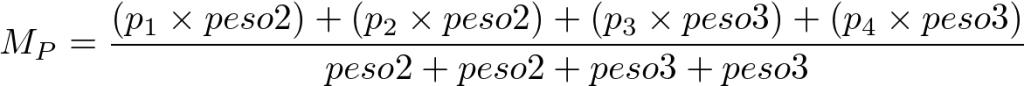
Onde:
- p1: prova 1
- p2: prova 2
- p3: prova 3
- p4: prova 4
Média final de João:
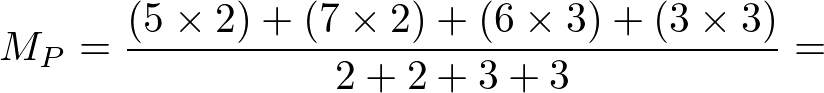
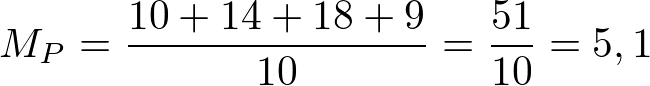
Considerando que o colégio adota a média final como 5 para ser aprovado, neste caso o aluno João foi aprovado com 5,1 de média final.
A média aritmética ponderada é bastante utilizada para calcular a média das notas de alunos nas escolas, vestibulares, concursos, etc. Geralmente, utiliza-se pesos para aplicar maior valor a um determinado conteúdo.
Por exemplo, num concurso a banca pode colocar um peso maior no conteúdo específico de cada vaga, pois é o mais importante a ser cobrado.
Exercícios respondidos de vestibulares
(UNIFESP) Para ser aprovado num curso, um estudante precisa submeter-se a três provas parciais durante o período letivo e a uma prova final, com pesos 1, 1, 2 e 3, respectivamente, e obter média no mínimo igual a 7.
Se um estudante obteve nas provas parciais as notas 5, 7 e 5, respectivamente, a nota MÍNIMA que necessita obter na prova final para ser aprovado é
- A) 9
- B) 8
- C) 7
- D) 6
- E) 5
Resolução:
Temos claramente o problema que envolve média ponderada, esse é um problema clássico que sempre cai em concursos, no ENEM e vestibulares.
Para responder essa questão, devemos multiplicar as notas das provas pelos seus respectivos pesos. A prova final não conhecemos a sua nota, sendo assim determinamos a variável x para essa nota.
Portanto,
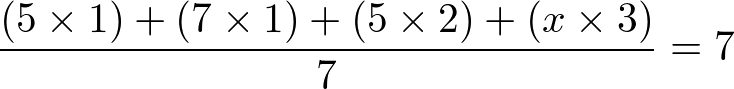
Onde x é a nota mínima que queremos encontrar para que a média seja igual a 7. Assim:
- 5 + 7 + 10 + 3x = 7 . 7 ⇒
- 22 + 3x = 49 ⇒
- 3x = 49 – 22 ⇒
- 3x = 27 ⇒
- x = 27⁄3 = 9
Logo, o aluno precisa tirar na prova final uma nota mínima 9 para passar de ano letivo, alternativa A.
(ENEM–1999) Um sistema de radar é programado para registrar automaticamente a velocidade de todos os veículos trafegando por uma avenida, onde passam em média 300 veículos por hora, sendo 55 km/h a velocidade máxima permitida. Um levantamento estatístico dos registros do radar permitiu a elaboração da distribuição percentual de veículos de acordo com sua velocidade aproximada.
A velocidade média dos veículos que trafegam nessa avenida é de
- A) 35 km/h
- B) 44 km/h
- C) 55 km/h
- D) 76 km/h
- E) 85 km/h
Resolução:
Temos no gráfico dados estatísticos que mostram o registro de velocidades dos veículos em um radar.
Para calcularmos a velocidade média dos veículos, temos que multiplicar cada um dos dados pelo valor percentual dado, depois somar os valores do produto e por fim dividir pelo soma dos valores percentuais.
Portanto,
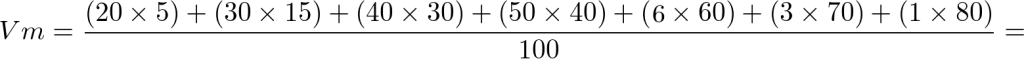
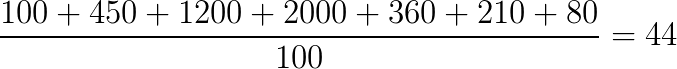
Logo a velocidade é de aproximadamente 44 km/h, alternativa B.
Exercícios Propostos
Veja os exercícios propostos no link a seguir:
Boa sorte!
Veja mais…
Encontrou algum erro? Nos avise clicando aqui
by