O conjunto dos números reais são formados por todos os números com representação decimal, ou seja, que tem casas decimais exatas ou periódicas (racionais) e as decimais não exatos e não periódicas (irracionais).
O símbolo que representa o conjunto dos números reais é o R.
Assim, o conjunto dos reais (R) é formado pela união do conjunto dos números racionais (Q) com o conjunto dos números irracionais (I).
Exemplos de números racionais (Q)
- 2
- 1⁄3
- 0,5555…
- 2,33
Exemplos de números irracionais (I):
- 1,2324233434…
- 5,03003000…
- √3
Subconjuntos do conjunto dos números reais
- R+ = conjunto dos reais não negativos, isto é, somente os números
positivos.
- Exemplo: R+ = {x ∈ R | x ≥ 0
- R– = conjunto dos reais não positivos, isto é, somente os números
negativos.
- Exemplo: R– = {x ∈ R | x ≤ 0}
- R* = conjunto dos reais não nulos, isto é, sem o zero.
- Exemplo: R* = {x ∈ R | x < 0 e x > 0}
- R*+ = conjunto dos reais positivos não nulos.
- R*+ = {x ∈ R | x > 0}
- R*– = conjunto dos reais negativos não nulos.
- R*– = {x ∈ R | x < 0}
O conjunto dos reais também incluem os conjuntos dos números naturais (N), Inteiros (Z), Racionais (Q) e Irracionais (I), portanto, eles também são subconjuntos dos reais.
- O conjunto dos números naturais (N): N = {0, 1, 2, 3, 4, 5, … }
- Conjunto dos números inteiros (Z): Z = {…, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, …}
- Conjunto dos números racionais (Q): Q = {…, 1⁄5, 2⁄3, –6⁄5, …}
- Conjunto dos números irracionais (I): I = {…, √3, √5, 3,141592, …}
Podemos verificar que os conjuntos citados acima são subconjuntos dos números reais através da observação da imagem abaixo:
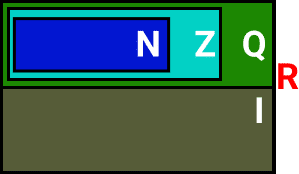
Então, podemos afirmar que:
- N ⊂ Z ⊂ Q ⊂ R
- I ⊂ R
Veja que R é igual a união de Q com I.
- R = Q ∪ I
Intervalos reais
Sejam a e b pertencente aos reais, com a < b, definimos:
Intervalo aberto nos extremos a e b é o conjunto:
]a, b[ = {x ∈ R | a < x < b}

Intervalo fechado nos extremos a e b é o conjunto:
[a, b] = {x ∈ R | a ≤ x ≤ b}

Intervalo fechado à esquerda e aberto à direita nos extremos a e b é o conjunto:
[a, b[ = {x ∈ R | a ≤ x < b}

Intervalo fechado à direita e aberto à esquerda nos extremos a e b é o conjunto:
]a, b] = {x ∈ R | a < x ≤ b}

Também podemos definir no conjunto dos números reais intervalos infinitos, veja:
]–∞, a[ = {x ∈ R | x < a}

]–∞, a] = {x ∈ R | x ≤ a}

]a, +∞[ = {x ∈ R | x > a}

[a, +∞[ = {x ∈ R | x ≥ a}

Leia também…



