Os números irracionais formam o conjunto dos irracionais identificado pelo símbolo I (maiúscula). Este conjunto é formado pelos números decimais, infinitos e não periódicos.
Os números irracionais não podem ser escritos na forma de fração em que o numerador e o denominador sejam números que pertencem ao conjunto dos números inteiros.
Exemplo de números irracionais:
- √5 = 2,23606797749978…
- √2 = 1,41421356237309…
- √7 = 2,64575131106459…
Apesar de os exemplos acima serem infinitos como uma dízima periódica, eles não podem ser escritos na forma de uma fração. Enquanto as dízimas periódicas podem ser escrita como uma fração.
Exemplo: 1,333333… = 4⁄3
Definição
Podemos definir o conjunto dos irracionais como:
I = {x ≠ a/b | a ∈ Z e b ∈ Z*}
Ou seja, os números de que estão contidos em I não podem ser frações com números inteiros. Então:
I = {…, -√2, …, e, … π, …}
Números irracionais notáveis
π (pi) é um famoso número usada na Geometria, ele é um número irracional, pois é infinito e não apresenta um período que se repete após a vírgula. Foi descoberto através da divisão do comprimento pelo diâmetro de uma circunferência.
π = 3,14159265358979…
O número de Neper é considerado um número irracional. É simbolizado pela letra e.
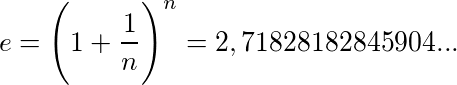
O número áureo, também conhecido como número de ouro, é uma proporção entre duas razões encontradas em elementos da natureza. Muito utilizado em obras de artes e construções. É denotado pela letra grega Φ (Phi).
Φ = 1,6180339
Números reais e números irracionais
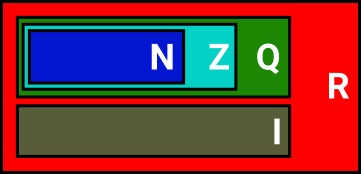
O conjunto dos números reais é formado pela união dos números racionais e dos irracionais.
Sabe-se que o conjunto dos números racionais contém todos os números que não são irracionais: números naturais e números inteiros. Por isso que os números reais são a união dos números racionais e irracionais
- R = Q ∪ I
- Q ∩ I = ∅
Vejamos na imagem a formação dos números reais. Veja que os irracionais é um conjunto a parte dentro dos reais.
Geometria e os números irracionais
Nos estudos da Geometria os irracionais foram o divisor de água quando se deu sua descoberta, pois muitos problemas sem respostas puderam ser solucionados, sem precisar ficar apresentando um resultado aproximado.
O teorema de Pitágoras, por exemplo, em que podemos calcular a hipotenusa a partir dos quadrados dos catetos, temos que o valor da hipotenusa será um número irracional. Veja:
Se considerarmos um quadrado de lado 1 x 1, temos que a medida da sua diagonal é:
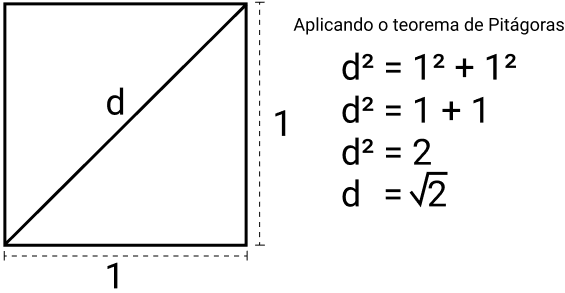
Portanto, temos que a média da diagonal é um número irracional √2. Se obtermos a sua raiz quadrada temos que: √2 = 1,41421356237309… e, portanto, um número que é infinito sem formar um período.
Por isso que a descoberta dos irracionais foi um marco para a Geometria, problemas como esse podem ser calculado e expressar seu resultado sem ter que ficar tentando apresentar um resultado aproximado.
Observações
- Seja a irracional e r racional não nulo, então:
- a + r
- a.r
- a/r
- r/a
- São números que pertencem a I.
- Exemplos:
- √2 + 1
- 3√2
- √3/2
- 3/√5
- As operações de adição, subtração, multiplicação ou divisão entre irracionais podem
ter como resultado um número racional ou um número irracional.
- Exemplos:
- √2 + √3
- √2.√3 = √6
- √2 – √3
- √2/√3 = √6/3
- São números que pertencem a I.
-
Exemplos:
- √2 + (1 – √2) = 1
- √2.√8 = 4
- √2 – √2 = 0
- √8/√2 = 2
- São todos números racionais
Exercícios
Bons estudos!
Leia também



