Regra de três composta é usada para encontrarmos um valor desconhecido quando temos no problema mais de duas grandezas.
É similar a regra de três simples, porém, teremos que analisar mais de duas grandezas num mesmo problema.
Definição
Regra de três composta é um método empregado para descobrir um valor desconhecido de um problema matemático, envolvendo mais de duas grandezas proporcionais.
Uma destas grandezas possui um valor desconhecido chamado de incógnita.
Como resolver regra de três composta?
Como na regra de três simples devemos separar as grandezas inicialmente, da seguinte forma:
-
Separe as grandezas de mesma espécie, agrupando-as em uma tabela:
- Encontre os valores correspondentes de cada grandeza e agrupe-os em uma coluna na tabela. Lembrando que regra de três composta pode ter três ou mais grandezas num mesmo problema;
-
Montar a proporção isolando a gradeza que contém a incógnita:
- A razão da grandeza que contém a incógnita deve ficar de um lado da igualdade, e as outras razões das outras grandezas devem formar um produto do outro lado da igualdade;
-
Analise cada grandeza separadamente em relação à grandeza que contém a
incógnita:
- Para realizar este passo, o aluno deve analisar cada razão da proporção separadamente. Deve-se então diminuir um valor na razão que pretende analisar e verificar o comportamento na razão que contém a incógnita. Se ocorrer um comportamento inverso, a grandeza é inversamente proporcional, isto é, se ao aumentarmos um valor em uma das gradezas e na grandeza que contém a incógnita diminuir, teremos uma grandeza inversamente proporcional. Caso contrário será diretamente proporcional;
-
Inverta quando necessário caso tenhamos grandezas inversamente
proporcionais:
- As razões das grandezas que são inversamente proporcionais em relação à razão da grandeza que contém a incógnita devem ser invertidas, isto é, troque o numerador pelo denominador da mesma razão;
-
Resolva o problema:
- Resolva o problema realizando primeiro o produto da proporção que está de um lado da igualdade. Depois, quando tiver apenas uma razão em cada lado da proporção, multiplique de forma cruzada, ou seja, o numerador de uma razão da proporção deve ser multiplicado pelo denominador da outra razão, e vice-versa.
A tabela do primeiro passo deve ser montada agrupando as grandezas assim:
| Grandeza A | Grandeza B | Grandeza C | Grandeza D |
|---|---|---|---|
| a1 | b1 | c1 | d1 |
| a2 | b2 | c2 | d2 |
Veja que na tabela conhecemos dois valores de cada grandeza, em uma dessas grandezas possuem a incógnita, ou seja, o valor desconhecido que queremos encontrar para resolver o problema.
Os valores de cada grandeza formará uma razão na proporção montada.
Lembrando que estamos exemplificando quatro grandezas nessa tabela, porém usa-se regra de três composta para resolver problemas a partir de três grandezas.
Como identificar se as grandezas são direta ou inversamente proporcionais?
Em regra de três simples vimos que existem dois tipos de regra de três: diretamente proporcional e inversamente proporcional
Diretamente proporcional
Se todas as grandezas forem diretamente proporcionais em relação à grandeza onde está a incógnita, montamos a proporção assim:
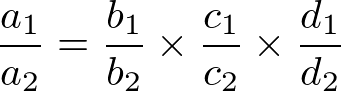
Quando todas as grandezas forem diretamente proporcionais, basta isolar a grandeza que contem a incógnita antes da igualdade e multiplicar as demais.
Neste caso, estamos considerando que a grandeza A tem a incógnita. Então a isolamos antes da igualdade.
Lembrando que uma grandeza é diretamente proporcional se ao aumentar ou diminuir um valor em uma das razões, na outra razão ocorre o contrário. Por exemplo, se uma diminui a outra aumenta, e vice-versa.
Inversamente proporcional
Quando alguma grandeza for inversamente proporcional em relação à grandeza onde está a incógnita, montamos a proporção assim:
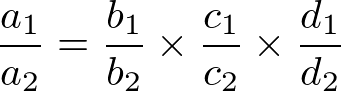
Considerando que a grandeza A tem a incógnita, isolamos ela antes da igualdade. Agora devemos analisar cada uma em relação à grandeza A.
Essa análise verifica se as grandezas são inversamente proporcionais. Isto é, vamos aumentar um valor em uma razão e verificar se também aumenta na outra razão também. Se aumentar em uma e diminuir na outra, temos grandezas inversamente proporcionais.
Caso a grandeza B for inversamente proporcional, montamos a proporção assim:
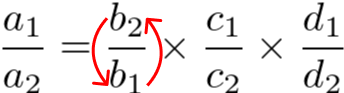
Invertemos a grandeza B, ou seja, trocamos o numerador com o denominador. Número de baixo vai para cima e o de cima vai para baixo.
Se a grandeza C for inversamente proporcional, motamos a proporção assim:

Aqui invertemos os valores da grandeza C, numerador e denominador foram trocados.
Se a grandeza D for inversamente proporcional, montamos a proporção assim:
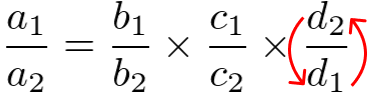
Aqui invertemos a grandeza D, trocando o numerador com o denominador.
Lembrando que uma grandeza é inversamente proporcional se ao diminuir ou aumentar um valor em uma razão, na outra razão ocorre o contrário. Por exemplo, se uma diminui a outra aumenta, e vice-versa.
Para não ficar dúvida, podemos ter mais de uma grandeza inversamente proporcional em relação à grandeza que contém a incógnita.
Exercícios Resolvidos
1) Sabendo que 4 operários constroem um muro de 30 m de comprimento em 10 dias, desde que eles trabalhem 8 horas diárias. Quantas horas por dia 6 operários deverão trabalhar para construir 45 m do mesmo muro em 8 dias?
Vamos resolver esse problema utilizando o passo a passo definido acima.
Separe as grandezas em um tabela
As grandezas desse problema são: operários, comprimento do
muro, dias e horas por dia
| Quantidade de operários | Comprimento do muro | Quantidade de dias | Horas por dia |
|---|---|---|---|
| 4 | 30 | 10 | 8 |
| 6 | 45 | 8 | x |
Montamos a proporção
Uma vez separada e agrupada as grandezas de mesma espécie em uma tabela, vamos montar a proporção para resolver o problema.
Para isso, devemos pegar a grandeza que contem o x (incógnita) e isolar de um lado da igualdade, enquanto as outras grandezas serão multiplicadas do outro lado da igualdade. Veja:

Analise separadamente as grandezas
Veja se são inversa ou diretamente proporcionais em relação à grandeza que contem o x, ou seja, a incógnita.
Caro leitor, você pode e deve utilizar setas guias para analisar o problema. Isto facilita quando resolvermos a proporção.
Inicialmente colocamos uma seta na razão que tem o x, ou seja, o valor que estamos procurando. Neste caso a seta independe do sentido, colocamos para baixo. Veja:

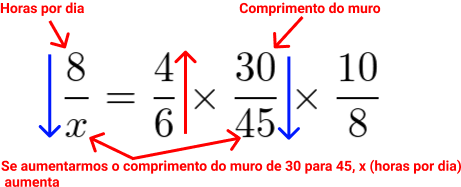
Analisando a grandeza operários em relação à grandeza horas por dias, temos que se aumentarmos o número de operários eles trabalharão menos horas por dias. Ou seja, aumentando um valor da razão de um lado da igualdade diminui na outra razão do outro lado.
Portanto, temos uma grandeza inversamente proporcional. Então coloquemos uma seta em sentido contrário.

Agora, analisando a grandeza comprimento do muro em relação à grandeza horas por dia, temos que se aumentarmos o comprimento do muro, o número de horas por dia que os operários devem trabalhar também aumenta.
Podemos pensar diferente, se esses operários trabalharem mais horas por dia, maior será o comprimento de muro que eles construirão.
Portanto, temos uma grandeza diretamente proporcional e, assim, a seta deve ter a mesma direção da grandeza que tem a incógnita. Veja:
Vamos analisar agora a última grandeza desse problema. Número de dias em relação à grandeza horas por dia.
Se diminuirmos o número de dias de 10 para 8, os operários deverão trabalhar mais horas por dia para construir o muro em 8 dias. Concorda?
Portanto, temos uma grandeza inversamente proporcional. Colocamos uma seta em sentido contrário a incógnita. Veja:

Inverta quando necessário caso tenhamos grandezas inversamente proporcionais
Para resolvermos o problema de forma correta, devemos inverter as grandezas com seta em sentido contrário a incógnita. Veja:
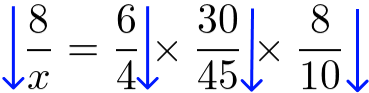
Resolva o problema
Como já fizemos todas as análises e montamos a proporção, vamos resolver o problema.
Primeiro devemos multiplicar na proporção abaixo o lado direito da igualdade. Isto é, devemos multiplicar as frações ou razões que estão do lado direito.

Feito a multiplicação, chegamos na seguinte proporção:
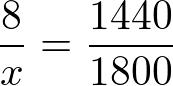
Por fim, basta multiplicarmos a proporção em cruz:

Logo, serão necessárias 10 horas por dia para construir 45 metros de muro em 8 dias.
Exercícios propostos
Veja também…



