Responda os exercícios de regra de três composta a seguir para fixar o aprendizado sobre o tema. Não consulte as respostas previamente.
1) Sabendo que 2 pedreiros constroem em cinco dias 320 metros de muro, quantos metros de muro serão construídos por 5 pedreiros trabalhando por um período de 8 dias?
Ver resposta
2 pedreiros —————— 320 m de muro —————- 5 dias
5 pedreiros —————— x metros de muro ————- 8 dias
Após separarmos as grandezas, montamos a proporção:
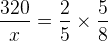
Todas as grandezas são diretamente proporcionais, aumentando o número de dias e de pedreiros a quantidade de metros também aumenta.
10x = 40 . 320 ⇒ 10x = 12800/10 ⇒ x = 1280
Então, 5 pedreiros constroem em 8 dias 1280 metros de muros
2) Para alimentar 20 ovelhas por um período de 8 dias, tem um custo de R$ 200 reais. Qual o custo para alimentar 30 ovelhas durante 2 dias?
Ver resposta
20 ovelhas ——— 8 dias ——– 200 reais de custo
30 ovelhas ——— 2 dias ——– x reais de custo
Se eu aumentar o número de ovelhas, teoricamente o custo deve aumentar, logo temos duas grandezas diretamente proporcionais. Se eu diminuir o número de dias, então o custo tende a diminuir. Logo, temos duas grandezas diretamente proporcionais.
Então basta montarmos a proporção.
Montando a proporção, temos o seguinte:
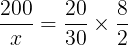
Resolvendo,
160x = 60 . 200 ⇒ 160x = 12000 ⇒ x = 12000/160 ⇒ x = 75.
Portanto, para alimentar 30 ovelhas em 2 dias teria um custo de R$ 75,00.
3) Uma fábrica de doces de leite produz 41000 potes de doces em 30 dias, com carga horaria de trabalho de 10 horas por dia. Quantos potes de doces a fábrica produzirá, se a carga horária diminuir para 8 horas por dia por um período de 15 dias?
Ver resposta
41000 potes de doces ———- 30 dias ———- 10 horas/dia
x potes de doces —————– 15 dias ———- 8 horas/dia
Se diminuirmos o número de dias, a fábrica produzirá menos potes de doces, logo temos duas grandezas diretamente proporcionais.
Se reduzirmos a quantidade de horas trabalhadas por dia, da mesma forma a fábrica produzirá menos potes de doces, então temos também duas grandezas diretamente proporcionais.
Montando a proporção:
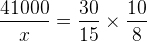
Resolvendo, chegamos ao seguinte resultado:
300x = 120 . 41000 ⇒ 300x = 4920000 ⇒ x = 4920000/300 ⇒ x = 16400
Logo, a fábrica produzirá 16.400 potes de doces de leite trabalhando durantes 15 dias, 8 horas por dia.
4) 18 operários com carga horária de trabalho de 7 horas por dia, faz um serviço em 12 dias. Se a carga horária for aumentada em 2 hora a mais por dia, 12 operários farão o mesmo serviço em quantos dias?
Ver resposta
18 operários ————- 7 horas/dia ————- 12 dias
12 operários ————- 9 horas/dia ————– x dias
Veja que a questão fala em aumento da carga horária em 2 horas, logo 9 horas por dia.
Se diminuirmos o número de operários, o número de dias trabalhado aumenta, assim temos duas grandezas inversamente proporcionais. Se aumentarmos o total de horas trabalhadas por dia, o número de dias diminui, então temos também duas grandezas inversamente proporcionais.
Fazendo a inversão, temos:
12 operários ————- 9 horas/dia ————- 12 dias
18 operários ————- 7 horas/dia ————– x dias
Montando a proporção:

Resolvendo, temos então o seguinte:
108x = 12 . 126 ⇒ 108x = 1512 ⇒ x = 1512/108 ⇒ x = 14
Portanto, se a carga horária for aumentada em 2 hora a mais por dia, 12 operários farão o mesmo serviço em 14 dias.
5) Realizar uma viagem entre duas cidades de carro dura cerca de 4 dias, com uma velocidade de 60 km/h, viajando por 8 horas diárias. Se a velocidade for aumentada para 100 km/h, e o tempo de viagem for de 5 horas por dia, quantos dias gastaríamos para ir de uma cidade à outra?
Ver resposta
4 dias ——– 60 km/h ——— 8 horas/dia
x dias ——– 100 km/h ——- 5 horas/dia
Vamos analisar. Se aumentar a velocidade, o número de dias diminui, então temos duas grandezas inversamente proporcionais. Se diminuirmos o total de horas viajadas, então o número de dias aumentam, logo temos também duas gradezas inversamente proporcionais.
Temos então que inverter as grandezas inversamente proporcionais.
4 dias ——– 100 km/h ——— 5 horas/dia
x dias ——– 60 km/h ———– 8 horas/dia
Montando a proporção, temos que:
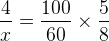
Resolvendo, temos então:
500x = 4 . 480 ⇒ 500x = 1920 ⇒ x = 1920/500 ⇒ x = 3,84
Portanto, aumentando a velocidade para 100 km/h, gastaríamos 3,84 dias para ir de uma cidade à outra viajando 5 horas por dia.
Para resolvermos exercícios de regra de três composta devemos ter em mente que temos que ter 3 ou mais grandezas envolvidas. Além disso, devemos analisar se as grandezas são inversamente ou diretamente proporcionais, e fazer a inversão quando for inversamente proporcionais.
Espero que os exercícios acima sirvam para fixar o aprendizado de regra de três composta.


