Conjuntos Numéricos: Subconjuntos e Intervalos

Conjuntos numéricos, na matemática, são os conjuntos que representam a classe dos números e são representados por 5 (cinco) grandes conjuntos:

O conjunto dos números reais, representado pela letra R, e contém todos os outros conjuntos;
O conjunto dos números irracionais, representado pela letra I, está contido no conjunto R;
O conjunto dos números racionais, representado pela letra Q, também está contido no conjunto dos números reais;
O conjunto dos números inteiros, representado pela letra Z, e está contido no conjunto Q e o conjunto R;
E, por fim, o conjunto dos números naturais, representado pela letra N, que, por sua vez, está contido nos conjuntos Z, Q, e R.

Podemos dizer também que o conjunto dos números naturais N é subconjunto de Z, sendo Z subconjunto de Q, que é subconjunto de R, logo N é subconjunto de Z, de Q, e de R.

Essa analogia é válida para Z que é subconjunto de Q, sendo Q subconjunto de R, logo Z é subconjunto de R. Apenas o conjunto dos números irracionais I é subconjunto de R.

Um conjunto é subconjunto de outro quando seus elementos são também elementos deste outro conjunto, ou seja, quando todos os elementos de um pertence ao outro.

Por exemplo, os elementos de N também são elementos de Z, de Q e de R. Tudo isso pode ser melhor visualizado na imagem abaixo, onde temos as relações de inclusão entre os conjuntos numéricos.

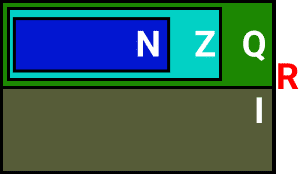
Pela imagem podemos ver a relação de inclusão dos conjuntos. Assim, podemos representar dessa forma: N ⊂ Z ⊂ Q ⊂ R, analogamente, também vale o seguinte, R ⊃ Q ⊃ Z ⊃ N; e I ⊂ R ou R ⊃ I.

Símbolos: ⊂ (está contido), e ⊃ (contém)

Conjunto dos números naturais (N)

O conjunto dos números naturais é representado pela letra N, contendo os números positivos incluindo o 0 (zero).

N = {0, 1, 2, 3, 4, 5, …}

É um conjunto infinito, não dá para representar todos os números, assim a reticência (…) indica que é um conjunto infinito. Também pode ser representado da seguinte forma:

N = {x ∈ N | x ≥ 0 }

Subconjuntos dos números naturais

Temos alguns conjuntos derivados do conjunto do números naturais, são eles:

N* = {1, 2, 3, 4, 5, …}; conjuntos dos números naturais não-nulos, ou seja, sem o zero;
N_p = {0, 2, 4, 6, 8, …}; conjunto dos números naturais pares;
N_i = {1, 3, 5, 7, 9; …}; conjunto dos números naturais ímpares;
P = {2, 3, 5, 7, 11, 13, …}; conjunto dos números naturais primos.

Todos esses conjuntos estão contidos no conjunto dos números naturais, e portanto são subconjuntos dele.

Conjunto dos números inteiros (Z)

O conjunto dos números inteiros é representado pela letra Z, contendo todos os números naturais e os números negativos, que são os números opostos aos positivos.

Z = {…, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5,…}

Também é um conjunto infinito nas duas extremidades.

Subconjunto dos números inteiros

Z* = {…, -5, -4, -3, -2, -1, 1, 2, 3, 4, 5,…}; conjunto dos números inteiros que não contem o zero, não-nulos;
Z₊ = {0, 1, 2, 3, 4, 5, …}; conjunto dos números inteiros positivos, isto é, sem os números negativos;
Z*₊ = {1, 2, 3, 4, 5, …}; conjuntos dos números inteiros positivos e sem o zero;
Z_– = {…, -5, -4, -3, -2, -1, 0}; conjunto dos números inteiros negativos;
Z*_– = {…, -5, -4, -3, -2, -1}; conjuntos dos números inteiros negativos e sem o zero.

Conjuntos dos números racionais (Q)

O conjunto dos números racionais é representados pela letra Q, contendo os números inteiros, forma decimal exata, os números na forma periódica ou na forma de fração.

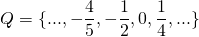
É um conjunto infinito também.

Números decimais na forma exata: Ex. {2,2; 5,432; 23,00009}

Números decimais na forma periódica: Ex. {3,2222…; 12,11111…; 40,12121212…}

Subconjunto dos números racionais (Q)

Q* conjuntos dos números racionais sem o zero;
Q₊ conjuntos dos números racionais positivos;
Q*₊ conjuntos dos números racionais positivos e sem o zero;
Q_– conjuntos dos números racionais negativos;
Q*_– conjuntos dos números racionais negativos e sem o zero.

Conjuntos dos números irracionais (I)

O conjunto dos números irracionais é representado pela letra I, contendo todos os números decimais não exatos e não periódicos.

Exemplos: 4,21315… ou 5,122030…

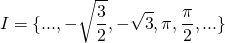
É um conjunto infinito.

Conjuntos dos números reais (R)

O conjuntos dos números reais é representado pela letra R, contendo todos os os conjuntos anteriormente citados. Assim, R é a união dos conjuntos N, Z, Q e I.

Subconjunto dos números reais

R* conjunto dos números reais sem o zero;
R₊ conjunto dos números reais positivos;
R*₊ conjunto dos números reais e sem o zero;
R_– conjunto dos números reais negativos;
R*_– conjunto dos números reais negativos e sem o zero.

Intervalos numéricos

Uma maneira de representar conjuntos numéricos na matemática é através dos intervalos numéricos. É importante lembrar que só é possível representar intervalos numéricos para os conjuntos e subconjuntos do conjuntos dos números reais.

Veja a seguir os tipos de intervalos:

Intervalos com extremos abertos

]a,b[ = {x ∈ R│a < x < b}

Intervalos com extremos fechados

[a,b] = {x ∈ R│a ≤ x ≤ b}

Intervalos aberto à direita e fechado à esquerda

[a,b[ = {x ∈ R│a ≤ x < b}

Intervalos aberto à esquerda e fechado à direita

]a,b] = {x ∈ R│a < x ≤ b}

Exercícios

Acesse os exercícios no link a seguir:

Exercícios com os conjuntos numéricos

Bons estudos!

Leia também
Razão e Proporção
Subtração de Frações
Números Primos
Regra de Três Composta
Critérios de Divisibilidade
Porcentagem
Tabuada