Subtração de frações é um pouco mais complicado do que a multiplicação e a divisão de frações. No entanto, não é difícil de aprender.
Subtrair frações é uma maneira de simplificar duas ou mais frações. O resultado é outra fração obtida através da subtração das frações anteriores.
Fique tranquilo, com a prática tudo fica claro. Antes de continuar lendo este artigo tenha em mente que você saiba calcular o MMC. Feito isso, podemos continuar.
Como subtrair frações?
Existem dois casos que podem aparecer durante o processo de subtrair duas ou mais frações: frações com denominadores iguais ou frações com denominadores diferentes.
Subtração de frações com denominadores iguais
Subtrair frações com denominadores iguais é bem fácil. Veja um exemplo:
Considere as frações:
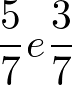
Vamos fazer a diferença:
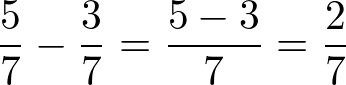
Dessa forma, mantemos o denominador (o número de baixo) e subtraímos os numeradores (números de cima).
Veja outro exemplo:
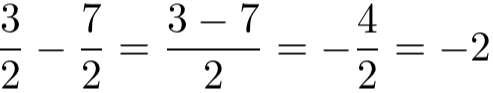
Lembrando que qualquer número natural pode ser representado como uma fração. Então, -2 = –2⁄1
Subtração de frações com denominadores diferentes
Nessa etapa é necessário calcular o MMC (mínimo múltiplo comum). Ou seja, precisamos encontrar um valor que é o mínimo múltiplo comum entre os dois ou mais denominadores das frações.
Considere as frações:
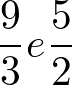
Vamos fazer a diferença entre elas:
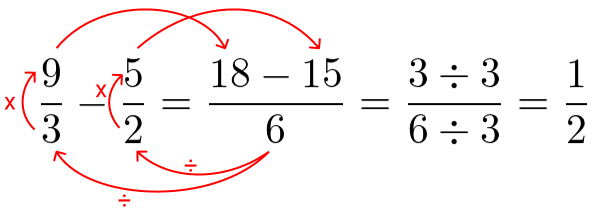
O primeiro passo foi encontrar o MMC de 3 e 2 que é 6.
Depois dividimos 6 pelo denominador da primeira fração e multiplicamos pelo numerador também da primeira fração: 6 ÷ 3 = 2 x 9 = 18.
Depois dividimos 6 pelo denominador da segunda fração e multiplicamos pelo numerador também da segunda fração: 6 ÷ 2 = 3 x 5 = 15.
Por fim, subtraímos os numeradores: 18 – 15 = 3. Assim, temos como resultado 3⁄6 que pode ser simplificado. Então, dividimos o numerador e denominador por 3, temos então uma fração irredutível.
Bem simples, a dificuldade é encontrar o MMC.
Como subtrair varias frações?
Não tem nenhuma diferença subtrair duas ou várias frações. O processo é o mesmo. Temos, apenas, que encontrar o MMC — denominador comum — para todas as frações. Vamos ver como funciona:
Considere as frações:
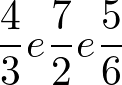
Vamos resolver esse problema:
Primeiro vamos calcular o MMC entre 3, 2 e 6.
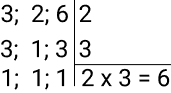
Dividimos pelo menor número possível com exceção do 1. Neste caso foi o 2, depois dividimos por 3. Quando encontramos resto 1, acaba. O MMC é a multiplicação dos números que dividimos, neste caso 2 e 3. Portanto, o MMC de 3, 2 e 6, é 6.
Perfeito, agora é só subtrair as frações. Veja:
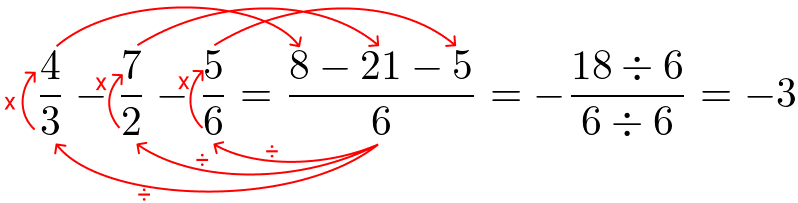
O que fizemos foi dividir 6 por 3 e multiplicar por 4, na primeira fração: 6 ÷ 3 = 2 x 4 = 8.
Depois dividimos 6 por 2 e multiplicamos por 7, na segunda fração: 6 ÷ 2 = 3 x 7 = 21.
Por fim, na terceira e última fração dividimos 6 por 6 e multiplicamos por 5: 6 ÷ 6 = 1 x 5 = 5. Sempre conservando o sinal.
Subtraímos os numeradores (8 – 21 – 5 = – 18) e encontramos o resultado. Como 18 é divisível por 6 temos como resultado -3.
É isso aí!
Antes de você ir, responda os exercícios propostos abaixo para fixar o aprendizado.
Exercícios propostos sobre subtração de frações
Veja mais…



