Soma de frações precisa de um pouco mais de conhecimento e dessa forma é um pouco mais trabalhosa do que multiplicação e divisão de frações.
Somar frações é uma forma de simplificar duas ou mais frações encontrando outra fração como o resultado da soma das frações anteriores.
Mas não se assuste, só precisamos praticar um pouco e tudo fica bem fácil.
Antes de continuar, tenha em mente que você saiba como calcular o MMC de dois números.
Após isso vamos continuar.
Como somar frações?
Existem basicamente duas formas de somar frações: frações com denominadores
iguais e frações com denominadores diferentes. Vamos ver
cada uma delas para você entender perfeitamente.
Soma de frações com denominadores iguais
Somar frações com denominadores iguais é bem simples. Veja um exemplo:
Considere as frações:
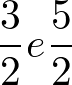
Vamos somá-las:
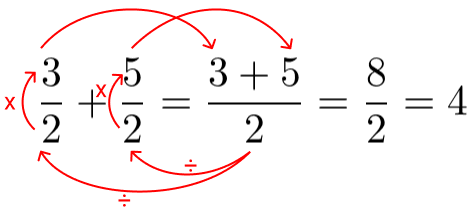
Como as frações possuem denominadores iguais não precisamos calcular o MMC.
Dessa forma, ao somar frações com denominadores iguais mantemos o denominador (número de baixo de cada fração) e somamos os numeradores (números de cima de cada fração).
Se for o caso, a fração deve ser simplificada para encontrar uma fração
irredutível, como no exemplo, encontramos
8⁄2 que é igual
4. Você pode estar perguntando: “E 4 é fração?”. Sim, 4 =
4⁄1,
todo número natural pode ser representado como uma fração.
Soma de frações com denominadores diferentes
Somar frações com denominadores diferentes necessita saber calcular o MMC (mínimo múltiplo comum) entre dois números. Veja um exemplo:
Considere as frações:
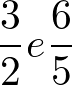
Vamos somá-las:
Como as frações possuem denominadores diferentes, nesse exemplo foi necessário encontrar o menor valor que é múltiplo para os denominadores (números de baixo) das frações.
O MMC de 2 e 5 é 10. Veja:
Relembrando como calcular o MMC.
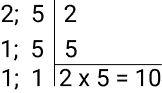
Encontramos o menor número que divide pelo menos um dos dois números, que é 2. Dividimos 2 e conservamos 5. Depois só o próprio 5 divide ele, além do 1. Dividimos e temos resto 1.
Agora, o MMC é a multiplicação dos números que dividimos, que é 10.
Após encontrarmos o MMC para 2 e 5, que é 10. Agora 10 passa a ser o denominador comum
para às duas frações. Veja na imagem abaixo:
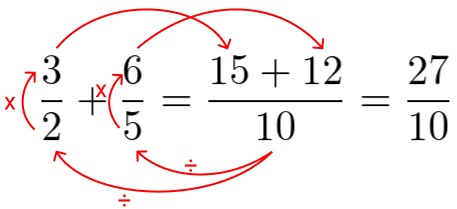
Para resolver esse problema, colocamos o 10 como denominador e vamos encontrar os numeradores para essa nova fração com denominador comum.
Assim, basta dividirmos 10 pelo denominador (número de baixo), 2, da primeira fração e multiplicamos com o numerador (número de cima), 3, também da primeira fração.
Depois fizemos o mesmo processo com a segunda fração. Dividimos 10 pelo denominador 5 e multiplicamos pelo numerador 6.
Por fim, somamos os resultados obtidos neste processo e teremos nessa soma o valor que vai ao numerador do resultado, que nesse caso foi 15 + 12 = 27.
É tranquilo, não é? A dificuldade aqui é encontrar o MMC.
Como somar varias frações?
O processo para somarmos várias frações funciona da mesma forma. Temos, apenas, que encontrar o MMC – denominador comum – para todas as frações. Vamos ver como funciona:
Considere as frações:
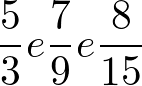
Vamos somá-las:

O que fizemos foi calcular o MMC para 3, 9 e 15, que é 45.
Depois colocamos 45 como denominador comum. O próximo passo foi dividir 45 por 3 e multiplicar por 5 na primeira fração:
45 / 3 = 15 x 5 = 75.
Então, de novo dividimos 45 por 9 na segunda fração e multiplicamos por 7:
45 / 9 = 5 x 7 = 35.
Por fim, dividimos 45 por 15 na terceira fração e multiplicamos por 8:
45 / 15 = 3 x 8 = 24.
Pronto, agora é só somar os números e acabou. UFA!
Antes de você ir, responda os exercícios propostos abaixo para fixar o aprendizado.
Exercícios propostos sobre soma de frações
Veja mais…



