A área do trapézio é a medida correspondente a superfície dessa figura da geometria plana. O cálculo da sua área é o produto entre a soma das medidas das bases pela altura, e dividindo o resultado por 2.
O trapézio possui quatro lados, por isso ele é também um quadrilátero. Dois lados são as bases, as bases são paralelas entre si. A base de maior medida é chamada de base maior, e a base de menor medida é chamada de base menor.
Índice do Artigo
Tipos de Trapézio
Podemos classificar os trapézios de acordo com suas formas e disposição no plano:
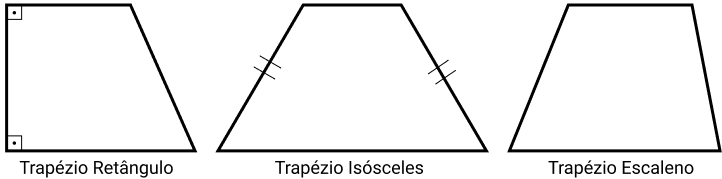
- Trapézio Retângulo: possui dois ângulos retos (90°). Além disso, o lado que possui os ângulos retos é perpendicular as bases. E é também a altura do trapézio.
- Trapézio Isósceles: possui dois lados com as mesmas medidas;
- Trapézio Escaleno: todos os lados com medidas diferentes.
Exemplo:
Como Calcular a Área do Trapézio?
A área do trapézio é calculada somando-se as bases menor e maior, multiplicando o resultado dessa soma pela altura, e dividindo por 2. Dessa forma, a fórmula que calcula a área do trapézio é:
Onde:
- A: é a medida da área;
- B: é a medida da base maior;
- b: é a medida da base menor;
- h: é a medida da altura.
Como Calcular o Perímetro do Trapézio?
O perímetro do trapézio é calculado somando-se todas as medidas de seus lados. Assim, a fórmula para calcular o perímetro é:
P = B + b + L1 + L2
Onde:
- P: é o perímetro do trapézio;
- B: é a medida da base maior;
- b: é a medida da base menor;
- L1 e L1: são os lados do trapézio.
Exercícios Resolvidos
Seja um trapézio medindo 3 cm de altura, base maior medindo 8 cm e base menor medindo 5 cm. Calcule a área do trapézio.
Resolução:
Dados:
- altura: 3 cm
- base maior: 8 cm
- base menor: 5 cm
Aplicando a fórmula:
- A = ((B + b) . h) / 2 ⇒ A = ((8 + 5) . 3) / 2 ⇒ A = 19,5 cm²
Determine a medida da base maior do trapézio com as seguintes medidas: altura, 2 cm; base menor, 4 cm e a área do trapézio igual 30 cm².
Resolução:
Dados:
- altura: 2 cm
- base menor: 4 cm
- área: 30 cm²
Aplicando a fórmula:
- A = ((B + b) . h) / 2 ⇒ 30 = ((B + 4) . 2) / 2 ⇒ 30 = (2B + 8) / 2 ⇒ 30 = B + 4 ⇒ 30 – 4 = B ⇒ B = 26 cm
Encontre a altura de um trapézio sabendo que as bases menor e maior medem, respectivamente, 5 cm e 10 cm e a área igual a 100 cm².
Resolução:
Dados:
- base menor: 5 cm
- base maior: 10 cm
- área: 100 cm²
Aplicando a fórmula:
- A = ((B + b) . h) / 2 ⇒ 100 = ((10 + 5) . h) / 2 ⇒ 100 = 15h / 2 ⇒ 100 = 15h / 2 ⇒ 200 = 15h ⇒ h = 200⁄15 ⇒ h = 13,33 cm
Exercícios Propostos
Acesse os exercícios no link a seguir:
Encontrou algum erro? Nos avise clicando aqui
by