A ideia de semelhança de triângulos em figuras planas na Geometria é de suma importância. Duas figuras são semelhantes quando elas possuem ângulos congruentes e lados proporcionais. Para indicar semelhança na matemática usamos a notação ~.
Definição
Seja dois triângulos ABC e A’B’C’, eles são semelhantes se, e somente se, as medidas dos ângulos sejam congruentes (medidas iguais) e as medidas dos lados respectivos sejam proporcionais.
Exemplo:
Os triângulos ABC e A’B’C’ da figura a abaixo são semelhantes, pois possuem ângulos correspondentes com medidas iguais.

Assim, podemos afirmar que:
Δ ABC ~ Δ A’B’C’ ⇔
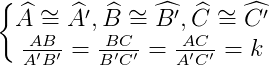
O número k é um valor constante e é chamado de razão de semelhança.
Casos de Semelhança de Triângulos
Apesar da definição informar que se dois triângulos são semelhantes eles possuem ângulos congruentes e lados proporcionais, não precisamos verificar todas essas propriedades para conferir todas as condições.
Veja, então, os três casos que garante a semelhança entre os triângulos:
Critério (AA~: Ângulo – Ângulo): Quando possuem dois pares de ângulos correspondentes congruentes, então eles são semelhantes.
Exemplo:
Seja os triângulos ABC e A’B’C’ abaixo:

Se os ângulos correspondentes possuem as mesmas medidas, então podemos afirmar que:
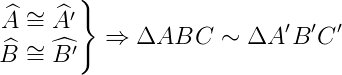
Critério (LAL~: Lado – Ângulo – Lado): Se dois lados de um triângulo tem medidas proporcionais a medida de dois lados de outro triângulo e os ângulos entre esses lados são congruentes, então eles são semelhantes.
Exemplo:
Seja os triângulos ABC e A’B’C’ abaixo:

Se pelo menos dois ângulos correspondentes são congruentes e dois lados correspondentes são proporcionais, então podemos afirmar que:
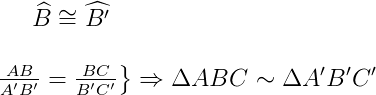
Critério (LLL~: Lado – Lado – Lado): Se dois triângulos possuem as medidas relativas aos três lados correspondentes proporcionais, então eles são semelhantes.
Exemplo:
Seja os triângulos ABC e A’B’C’ abaixo:
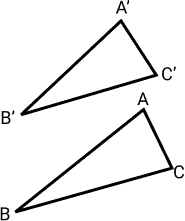
Se todos os lados dos triângulos possuem medidas proporcionais, então podemos afirmar que:
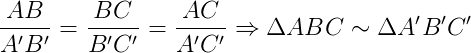
Razão de Semelhança
A razão que define a semelhança entre dois triângulos é a razão entre as medidas dos lados correspondentes.
Dessa forma, se a razão de semelhança entre dois triângulos é um número k, então a razão entre dois elementos dos triângulos será k.
Isto quer dizer que se a razão de semelhança entre dois triângulos é 5, a razão entre as medianas correspondentes será 5, a razão entre as alturas será 5, e assim por diante.
Exemplo:
Seja os triângulos ABC e ADE abaixo:

Onde:
- AQ e AP são as alturas.
- AM e AN são as medianas.
Com isso, temos que a razão de semelhança do triangulo ABC para o triângulo ADE é o número k, de forma que k seja proporcional as medidas referentes a altura, medianas e dos lados do triângulo, entre outros.
Então, podemos afirmar que:
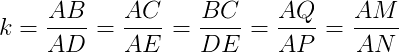
Teorema Fundamental
O teorema fundamental da semelhança diz que se traçarmos uma reta paralela a um dos lados de um triângulo, essa reta intercepta os outros dois lados do triângulo em pontos diferentes. O triângulo formado é semelhante ao triângulo original.
Veja na figura abaixo que o triângulo ABC é cortado por uma reta r é paralela ao lado BC.
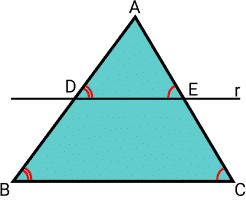
Para verificar que os triângulos são semelhantes, devemos observar se o triângulo original é semelhante ao triângulo formado pela reta r.
Ao observar a imagem acima, percebe-se que os ângulos B e D e também E e C são semelhantes pois DE // BC, de acordo com o postulado das retas paralelas.
Como o ângulo A é um ângulo comum aos dois triângulos, temos que os ângulos são congruentes para os dois triângulos.
Portanto, pelo critério (AA), os triângulos ABC e ADE são semelhantes.
Para saber mais leia sobre o Teorema de Tales.
Casos de Congruência de Triângulos
Semelhança de triângulos é diferente de igualdade entre os triângulos. Assim, para verificar se dois triângulos são iguais devemos observar os seguintes casos:
- Os triângulos possuem lados com medidas iguais.
- Dois lados dos triângulos possuem medidas iguais, assim como o ângulo correspondente também possui a mesma medida.
- Dois ângulos dos triângulos possuem medidas iguais e o lado entre esses ângulos tenha a mesma medida.
Relações Métricas no Triângulo Retângulo
Os triângulos retângulos são os triângulos que possuem um ângulo reto, ou seja, ângulo que mede 90°.
No triângulo ABC abaixo, a altura h, relativa à hipotenusa divide o triângulo em dois triângulos retângulos.
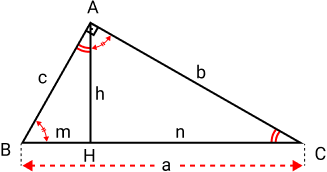
Como os triângulos ABC, ABH e ACH possuem um ângulo que mede 90°, e os lados AB e AC, AH e CH e AH e BH são proporcionais, então podemos afirmar que os triângulos são semelhantes, pelo critério LAL~. Logo: ABC ~ ABH ~ ACH.
Dessa forma, como as medidas dos lados são proporcionais temos as seguintes relações entre as medidas dos lados:
| Relações Métricas no Triângulo Retângulo |
|---|
| b² = a . n |
| c² = a . m |
| a² = b² + c² |
| h² = m . n |
| b . c = a . h |
Estude mais sobre as relações métricas no triângulo retângulo e também sobre o Teorema de Pitágoras.
Exercícios
Acesse os exercícios no link a seguir:



