Responda os exercícios a seguir para entender como identificar e resolver exercícios sobre semelhança de triângulos.
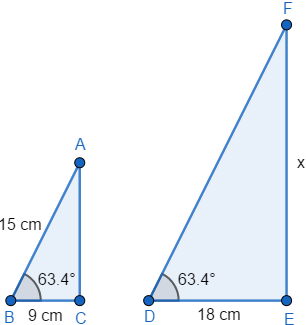
1) Calcule o valor de x para os triângulos abaixo:
Ver resposta
Observando a figura da questão podemos verificar que os triângulos são semelhantes pelo critério AA~ (ângulo – ângulo).
O lado AC do triângulo menor é o lado correspondente ao lado FE do triângulo maior, com medida x. Vamos encontrar a medida do lado AC utilizando o teorema de Pitágoras.
15² = 9² + (AC)² ⇒
225 = 81 + (AC)² ⇒
(AC)² = 225 – 81 ⇒
AC = √144 ⇒
AC = 12
Portanto, a medida do lado AC é igual a 12 cm.
Agora podemos encontrar a medida do lado x já que os lados são proporcionais, fazenda a seguinte proporção:
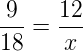
Resolvendo, temos que:
9x = 12 . 18 ⇒
9x = 216 ⇒
x = 216/9 ⇒
x = 24
Logo, a medida de x é igual a 24 cm.
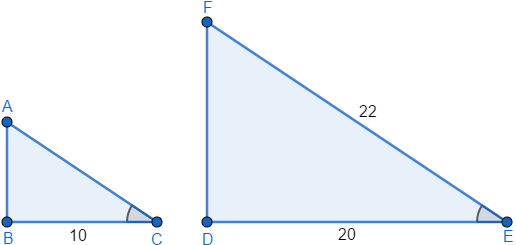
2) Determine a medida do lado AB:
Ver resposta
Os triângulos da questão são semelhantes pelo critério AA~ (ângulo – ângulo), pois possuem dois ângulos com a mesma medida.
Dessa forma, vamos calcular a medida do lado AC já que os lados correspondentes são proporcionais, assim:
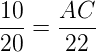
Resolvendo, temos:
AC . 20 = 10 . 22 ⇒
AC . 20 = 220 ⇒
AC = 220/20 ⇒
AC = 11
Portanto, a medida relacionada ao lado AC é 11.
Agora, para encontrarmos a medida relacionada ao lado AB vamos utilizar o teorema de Pitágoras.
(AC)² = (AB)² + (BC)² ⇒
11² = (AB)² + 10² ⇒
121 = (AB)² + 100 ⇒
(AB)² =121 – 100 ⇒
AB = √21 ⇒
AB = 4,6
3) Determine a altura do prédio da imagem a seguir, sabendo que os lados EC e FG são perpendiculares a CD; e EC e FG são paralelos entre si.
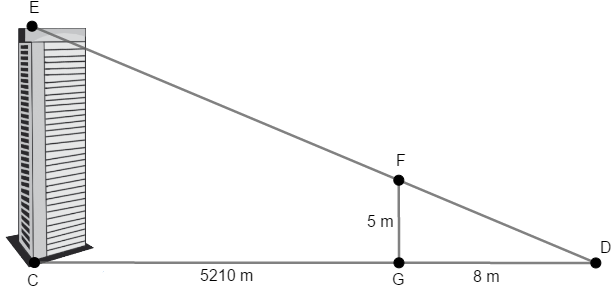
Ver resposta
Ao analisar a imagem da questão podemos identificar dois triângulos: CDE e DFG. Veja que a questão afirma que os lados FG e EC são paralelos entre si e perpendiculares a CD, temos então dois ângulos de 90°. Logo, os dois triângulos são semelhantes pelo critério AA~ (ângulo – ângulo).
Para determinarmos a medida da altura do prédio, precisamos determinar a medida do lado EC. Então:
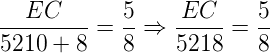
Resolvendo, temos então que:
EC . 8 = 5 . 5218 ⇒
EC . 8 = 26090 ⇒
EC = 26090/8 ⇒
EC = 3261,25
Portanto, a altura do prédio é de 3.261,25 metros.


