A trigonometria no triângulo retângulo permite determinar os elementos de um triângulo retângulo quando eles não são dados no problema. Estes elementos são: lados e ângulos.
Triângulo Retângulo
Os triângulos retângulos são aqueles que possuem um ângulo reto. Chamamos ângulo reto na Geometria Plana os ângulos que medem 90°. Os ângulos que medem menos de 90° são chamados agudos.
É importante lembrar que a soma das medidas internas dos ângulos de um triângulo qualquer é igual a 180°.
Como os triângulos retângulos possuem um ângulo reto, então os outros ângulos são, necessariamente, agudos, isto é, medem menos que 90°.
Por esse motivo, as medidas dos ângulos agudos são chamadas medidas complementares.
Exemplo:
Seja o triângulo ABC, retângulo em C, da figura seguir:
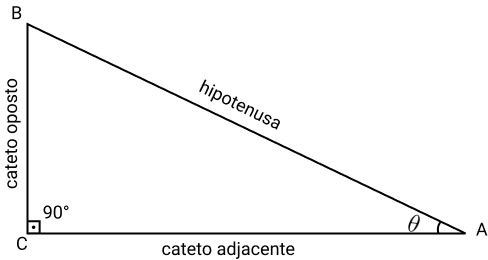
Os lados do triângulo retângulo são chamados de:
- Cateto Adjacente
- Cateto Oposto
- Hipotenusa
Em qualquer triângulo retângulo, os lados que formam o ângulo reto são chamados catetos, o lado oposto ao ângulo reto é chamado hipotenusa e os ângulos agudos são chamados complementares.
Teorema de Pitágoras
O Teorema de Pitágoras diz que:
A soma dos quadrados das medidas dos catetos é igual ao quadrado da medida da hipotenusa.
O enunciado acima é equivalente à fórmula:
a² = b² + c²
Onde:
- a é a hipotenusa;
- b e c são os catetos.
O Teorema de Pitágoras pode ser aplicado para encontrar as medidas dos lados de um triângulo retângulo quando conhecemos dois deles.
Leia mais sobre o Teorema de Pitágoras
Relações Trigonométricas no Triângulo Retângulo
Através da razão entre os lados do triângulo podemos definir as principais razões trigonométricas, são elas:
- Seno
- Cosseno
- Tangente
Exemplo:
Considere o triângulo ABC, reto em C, da figura seguir:
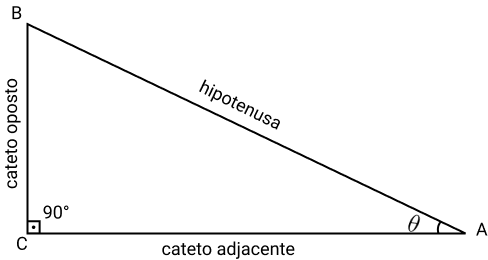
As razões trigonométricas básicas são obtidas através das relações entre os lados do triângulo. Vamos exemplificar cada uma delas.
Seno
O Seno de um ângulo agudo em todo triângulo retângulo é a razão entre a medida do cateto oposto a esse ângulo e a medida da hipotenusa.
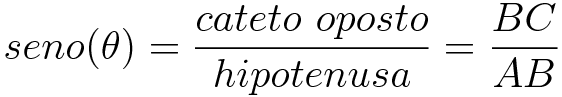
Cosseno
O Cosseno de um ângulo agudo em qualquer triângulo retângulo é a razão entre a medida do cateto adjacente a esse ângulo e a medida da hipotenusa.
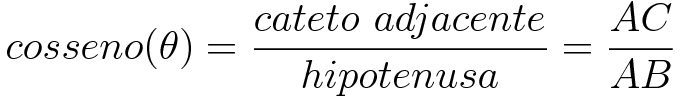
Tangente
A Tangente de um ângulo agudo em todo triângulo retângulo é a razão entre a medida do cateto oposto a esse ângulo e a medida do cateto adjacente a esse ângulo.

Leia mais sobre as razões trigonométricas
Ângulos Notáveis
Entre os ângulos agudos de um triângulo, existem três que aparecem com mais frequência em problemas de trigonometria evolvendo triângulos. Esses ângulos são chamados ângulos notáveis, são os de 30°, 45° e 60°. A tabela a seguir mostra as medidas deles.
| Relações Trigonométricas | 30° | 45º | 60° |
|---|---|---|---|
| Seno | 1/2 | √2/2 | √3/2 |
| Cosseno | √3/2 | √2/2 | 1/2 |
| Tangente | √3/3 | 1 | √3 |
Relações entre Seno, Cosseno e Tangente no Triângulo Retângulo
Seja o triângulo ABC, reto em A, com lados a, b e c da figura a seguir:

Observando a figura do triângulo acima podemos definir:
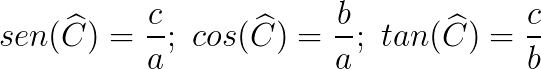
Dessa forma, se dividirmos:
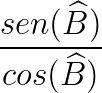
Obtemos:
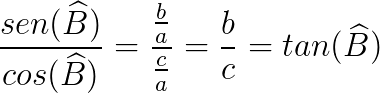
A tangente de um ângulo no triângulo é a razão entre o seno e o cosseno desse ângulo. Assim:
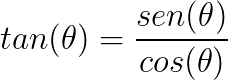
Agora se dividirmos o Teorema de Pitágoras a² = b² + c² por a², teremos:
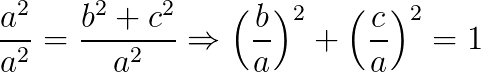
Se substituirmos:
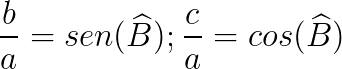
Obtemos:
sen²(B) + cos²(B) = 1
Dessa forma, concluímos que a soma do quadrado do seno e do cosseno é igual a 1.
Além disso, o sen(B) = cos(C) e sen(C) = cos(B).
Portanto, em relação aos ângulos agudos, concluímos que o seno desse ângulo é igual ao cosseno do complemento desse ângulo, e vice-versa.
Então, temos as seguintes expressões:
- sen²(θ) + cos²(θ) = 1
- cos(θ) = sen(90° – θ)
- sen(θ) = cos(90° – θ)
Exercício Resolvido
Seja os triângulos a seguir, determine as medidas dos senos, cossenos, tangentes dos ângulos agudos.
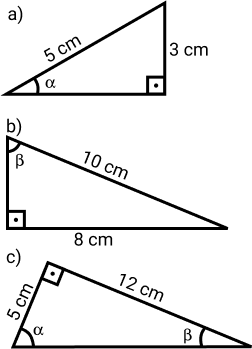
a)
O seno do ângulo α: sen(α) = 3⁄5 = 0,6
Para calcular o cosseno, precisamos do valor do cateto adjacente, para isso utilizaremos o Teorema de Pitágoras para encontrar a medida do lado.
a² = b² + c² ⇒ 5² = 3² + c² ⇒ 25 – 9 = c² ⇒ c = √16 = 4
Assim, o cosseno do ângulo α: cos(α) = 4⁄5 = 0,8
A tangente do ângulo α é: tan(α) = 3⁄4 = 0,75
b)
O seno do ângulo β: sen(β) = 8⁄10 = 0,8
Para calcular o cosseno, precisamos do valor do cateto adjacente, vamos utilizar o Teorema de Pitágoras.
a² = b² + c² ⇒ 10² = b² + 8² ⇒ 100 – 64 = b² ⇒ b = √36 = 6
Assim, o cosseno do ângulo β: cos(β) = 6⁄10 = 0,6
A tangente do ângulo β é: tan(β) = 8⁄6 = 1,3
c)
- Para α
Nessa alternativa precisamos encontrar o valor da hipotenusa, para isso utilizaremos o Teorema de Pitágoras para encontrar a medida do lado.
a² = b² + c² ⇒ a² = 5² + 12² ⇒ a² = 25 + 144 ⇒ a = √169 = 13
Então, o seno do ângulo α: sen(α) = 12⁄13 = 0,9
O cosseno do ângulo α: cos(α) = 5⁄13 = 0,4
A tangente do ângulo α é: tan(α) = 12⁄5 = 2,4
- Para β:
O seno do ângulo β: sen(β) = 5⁄13 = 0,4
O cosseno do ângulo β: cos(β) = 12⁄13 = 0,9
A tangente do ângulo β é: tan(β) = 5⁄12 = 0,4



