Equação do 1º grau (primeiro grau) é nada mais do que uma igualdade entre as expressões, que as transformam em uma identidade numérica, para um ou para mais valores atribuídos as suas variáveis.
Definição
É toda sentença aberta, redutível e equivalente a ax + b = 0, com a ∈ R* e b ∈ R.
Ou seja, a e b são números que pertencem ao conjunto dos números reais (R), com a diferente de zero e x representa uma variável que não conhecemos (incógnita).
A incógnita é o valor que precisamos achar para encontrar a solução para a equação. A variável que não conhecemos (incógnita) costumamos representá-la na equação pelas letras x, y e z.
Numa equação do primeiro grau, o expoente da incógnita é sempre 1.
Exemplo:
- 5 + x = 8
Essa equação se transforma numa identidade, fazendo:
- x = 3 ⇒ 5 + x = 8 ⇒ 5 + 3 = 8 ⇒ 8 = 8 temos uma identidade.
A letra x na equação é denominada a variável da equação ou incógnita, enquanto que o número 3 é chamado de solução da equação, conjunto verdade ou raiz.
Na equação acima, o que está antes da igualdade é chamado de primeiro membro, e o que está do lado direito é chamado de segundo membro da equação.
Exemplo:
- 3x – 12 (1º membro) = 7 + x (2º membro)
Tipos de equações
As equações podem ter uma ou mais incógnitas, ou variáveis, como queira chamar:
Exemplos:
- 4 + 2x = 11 + 3x (uma incógnita ou uma variável, a variável x)
- y – 1 = 6x + 13 – 4y (duas incógnitas ou duas variáveis, x e y)
- 8x – 3 + y = 4 + 5z – 2 (três incógnitas ou três variáveis, x,y e z)
Observação: não importa se a variável apareceu várias vezes, o que conta é quantas variáveis diferentes tem na equação.
Exemplo: x + 1 = x + 2, temos uma variável, o x, e não duas, não é a quantidade que consideramos.
Forma normal de uma equação
Uma equação está na forma normal quando todos os seus termos estão no primeiro membro reduzido e ordenado segundo as potências decrescentes de cada variável.
Exemplos:
- 5x – 20 = 0
Ou seja, todos os termos estão antes da igualdade (1º membro).
Classificação de uma equação do 1º grau (primeiro grau)
As equações algébricas podem ser racionais e irracionais.
Racionais: quando a variável não tem nenhum expoente fracionário, ou seja, quando a incógnita não está sob um radical. Caso contrário, são ditas irracionais.
Exemplo:
2x – 16 = 0 (racional)
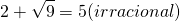
As equações racionais classificam-se em inteiras e fracionarias. São inteiras se todos os expoentes das incógnitas são números inteiros e positivos. Caso contrário, se existir uma incógnita no denominador ou, com expoente inteiro e negativo, a equação se diz fracionária.
Exemplo:
2x – 16 = 0 (racional inteira)
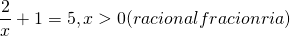
Equações equivalentes
Duas ou mais equações são equivalentes quando admitem a mesma solução ou mesmo conjunto verdade.
Exemplo:
- 3x – 9 = 0 ⇒ admites 3 como solução (ou raiz)
- 4 + x = 7 ⇒ admite 3 como solução (ou raiz)
Então podemos dizer que estas equações são equivalentes.
Equações numéricas
É a equação que não tem nenhuma outra letra diferente a não ser a das incógnitas.
Exemplo:
- x – 5 = -2x + 22
Equações literais
Toda equação que contém outra letra, além das que representam as variáveis.
Exemplo:
- 3ax – 5 = ax + 4 (variável é x)
Equações possíveis e determinadas
São as equações que admitem um número finito de soluções que, neste caso, por ser uma equação do 1º grau só admite uma única solução.
Exemplo:
- x – 2(x + 1) = -3 (admite somente o número 1 como solução)
- S = V = {1} conjunto unitário (conjunto que possui somente um elemento)
Equações possíveis e indeterminadas
Equações que admitem infinitas soluções, ou seja, um número infinito de soluções. Também denominada de identidades. Seu conjunto verdade é representado pelos números reais.
V = S = R (conjunto de todos os números reais)
Exemplo:
- 5x – 2y = 105 (admite infinitas soluções)
Equações impossíveis
São todas as equações que não admitem soluções. Seu conjunto solução é o conjunto vazio
Exemplo:
- x + 2 = x + 3 ⇒ x – x = -2 + 3 ⇒ 0 = 1
Não forma uma igualdade. Conjunto solução ou conjunto verdade é: V = S = {} = Ø (vazio)
Como resolver uma equação de primeiro grau?
Para resolver uma equação do primeiro grau deve-se levar em consideração que ao mudarmos as variáveis (incógnitas) e os valores numéricos de posição na equação, a igualdade deve continuar sendo verdadeira.
Também devemos ficar atento com o sinal de cada variável ou valor numérico, pois para que a igualdade continue valendo devemos inverter o sinal ao mudar de lado na equação, apenas quando se trata de uma adição ou subtração.
Dessa forma, uma multiplicação passa para o outro lado dividindo, uma divisão passa multiplicando, uma subtração passa somando e uma soma passa subtraindo. Veja:
Exemplo: Encontrar o valor de x na equação: 3x + 2 = x + 1
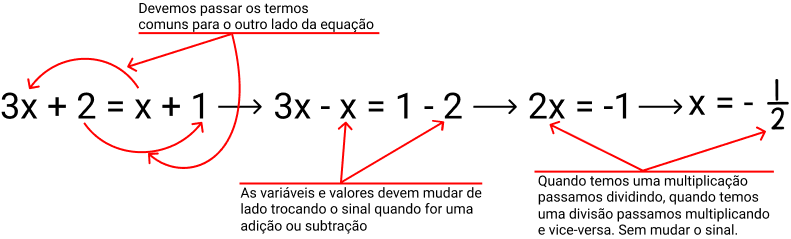
Dessa forma, o valor da variável x que torna a equação verdadeira é –1⁄2.
Vamos ver outro exemplo.
Exemplo: Encontrar o valor de x para a equação: -5x = -5
Existem duas formas de responder essa equação, multiplicando os dois lados por -1, para tornar toda a equação positiva ou manter o sinal e lembrar que durante a divisão de dois números negativos o sinal muda para positivo. Veja:
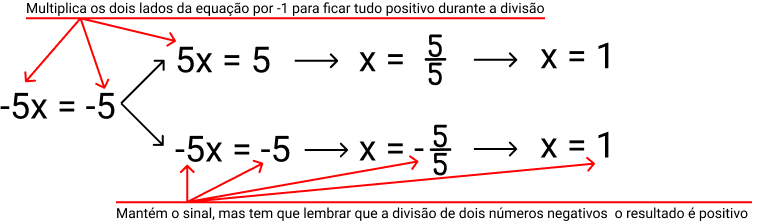
Atenção: sempre pode-se multiplicar os dois lados por -1, apesar de ser mais útil quando o lado que possui a incógnita for negativo.
Espero que tenha entendido. Bons estudos!
Exercícios Propostos
Leia também



