Equação do 2º Grau (Segundo Grau)

Uma equação do 2º (segundo grau) é uma equação com duas incógnitas x, sendo que uma delas possuem um grau igual a 2.

Definição

Chamamos de equação do segundo grau as equações do tipo ax² + bx + c = 0 com a, b e c ∈ R, onde a ≠ 0.

Os parâmetros da equação são:

• a – coeficiente principal
• b – coeficiente secundário
• c – termo independente

Exemplo:

• 2x² + 5x + 3 = 0 (essa é uma equação do segundo grau, veja o grau 2 na primeira incógnita)

Chamamos a, b e c de coeficientes, a é sempre coeficiente de x², b é sempre coeficiente de x, e c é sempre coeficiente do termo independente.

Exemplos:

• 3x² + 4x + 1 = 0: é uma equação do segundo grau, com a = 3, b = 4, c = 1.
• x² – x – 1 = 0: é uma equação com grau 2, com a = 1, b = –1, c = –1 .
• 9x² – 5x = 0: também é uma equação de grau 2, com a = 9, b = –5, c = 0.
• 5x² – 4 = 0: equação do segundo grau, com a = 5, b = 0, c = –4.

Formula de Bhaskara

Toda equação do segundo grau pode apresentar até duas soluções diferentes. Em todos os casos estas soluções podem ser obtidas pela fórmula de Bhaskara.

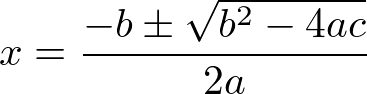
Raízes de uma equação do 2º grau

Para resolvermos uma equação do 2º grau é necessário que encontremos as raízes da equação. As raízes são valores que quando substituímos nas incógnitas, tornam a sentença verdadeira. Assim, as raízes da equação formam o conjunto solução ou o conjunto verdade da equação.

As soluções da equação do segundo grau são chamadas de raízes da equação, sobretudo por apresentar na fórmula de Bhaskara uma radiciação. São apresentadas de forma separadas por x₁ e x₂. Onde:

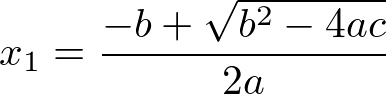
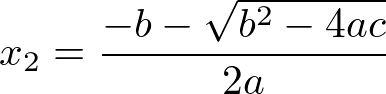
No radical da fórmula de Bhaskara temos b² – 4ac, chamado discriminante. Ele é representado pela letra grega maiúscula delta (Δ). O delta determina o total de soluções da equação do segundo grau no conjunto dos números reais.

Assim:

• Se Δ > 0, então a equação admite várias soluções em R;
• Se Δ = 0, então a equação admite uma única solução em R;
• Se Δ < 0, ou seja, Δ for negativo, a equação não admite solução em R.

Equação do 2º grau (segundo grau) completa e incompleta

Uma equação do 2º grau é chamada de completa quando os coeficientes b e c são diferentes de zero.

Exemplos:

• 2x² + 3x + 3 = 0
• x² + x + 1 = 0

São equações completas.

Uma equação do 2º grau é chamada de incompleta quando os coeficientes, b ou c, forem iguais a zero, basta um deles ser igual a zero, ou ambos serem iguais a zero.

Exemplos:

• x² – 3 = 0  (b = 0)
• 2x² + x = 0 (c = 0)
• 5x² = 0 (b = 0 e c = 0)

São equações incompletas.

Como resolver uma equação do segundo grau?

Para resolver uma equação de grau 2, precisamos identificar o tipo da equação. Se for completa, resolveremos de uma forma e se for incompleta resolveremos de outra forma. Vamos aprender todas elas.

Resolução de uma equação do segundo grau completa

Para resolver uma equação completa, a ideia é que comecemos a resolver pelo discriminante, e assim podemos resolver em dois passos a equação:

• Primeiro passo é encontrar o valor do discriminante: Δ = b² – 4ac

• Então o segundo passo só deve ser resolvido se o valor de discriminante for maior ou igual a zero. Caso seja, usamos a expressão:

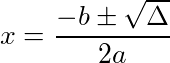
Se o valor do discriminante for negativo, não ha como realizar o segundo passo considerando o conjunto dos números reais. Portanto, a equação não possui uma solução real.

Vamos ver um exemplo:

Encontre a solução para a seguinte equação: x² – 5x + 6 = 0.

Resposta:

Observe que temos uma equação do segundo grau completa. Primeiro vamos encontrar os coeficientes da equação, isto é, os valores de a, b e c.

• x² – 5x + 6 = 0
  • a = 1
  • b = –5
  • c = 6

Vamos executar os passos para resolver essa equação:

Primeiro passo: (Δ = b² – 4ac)

• Δ = (-5)² – 4.1.6 = 25 – 24 = 1 (Δ > 0)

Como delta é maior que zero, vamos realizar o segundo passo.

Segundo passo: 

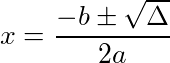
Temos que substituir na expressão acima os valores para os coeficientes a, b, e o resultado do cálculo do descriminante Δ. Logo,

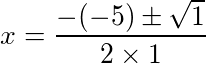
Agora temos que analisar em relação aos sinais de mais (+) e de menos (-). Para o sinal de mais vamos chamar a expressão de x₁ e para o sinal de menos vamos chamar de x₂.

Para x₁ temos:

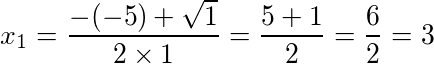
Para x₂ temos:

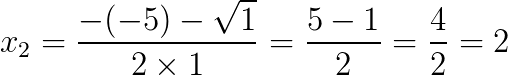
Na expressão já tínhamos o -b e ao adicionar o -5 ficou -(-5), então –(–5) = 5. E a raiz quadrada de 1 é 1, esse 1 vem do resultado do primeiro passo que foi o cálculo do descriminante Δ. No mais não há segredo.

Dessa forma, encontramos às duas raízes que formam o conjunto solução da equação dada neste exemplo. O conjunto solução que resolve a equação, que torna ela verdadeira.

Logo, S = {2, 3}

Veja:

Se substituirmos as raízes, veremos que elas realmente resolvem a equação.

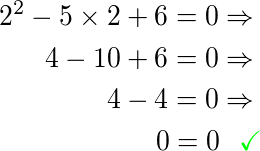
Temos uma igualdade para a raiz de número 2.

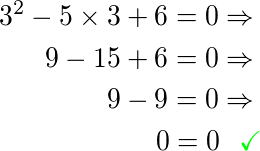
Também temos uma igualdade para a raiz de número 3. Portanto, encontramos realmente as raízes que resolvem essa equação.

Vamos ver outro exemplo para o caso em que Δ = 0.

Encontre as raízes da equação: 4x² – 4x + 1 = 0.

Pela equação temos os coeficientes:

• a = 4
• b = -4
• c = 1

Primeiro passo: vamos calcular o discriminante (Δ = b² – 4ac):

• Δ = (-4)² – 4 . 4 . 1 = 16 – 16 = 0

Segundo passo: substituir os valores na expressão:

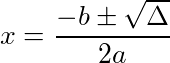
Substituindo os valores aos coeficientes correspondentes, temos:

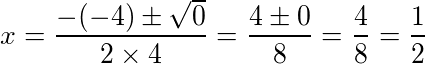
Portanto, S = {¹⁄₂}.

Perceba que quando Δ = 0 temos somente uma raiz que resolve a equação.

Vamos ver agora um exemplo para o caso em que Δ < 0, ou seja, Δ negativo.

Calcule as raízes da equação: 5x² + x + 6 = 0.

Os coeficientes da equação são:

• a = 5
• b = 1
• c = 6

Primeiro passo é calcular o Δ (Δ = b² – 4ac):

• Δ = 1² – 4 . 5 . 6 = 1 – 120 = -119

Como temos Δ < 0, ou seja, o valor do descriminante é negativo, não conseguiremos realizar o segundo passo. Dessa forma, não há como encontrar raízes para essa equação no conjunto dos reais.

Portanto, o conjunto solução para essa equação é vazio: S = {} = Ø

Para finalizar vamos resolver um problema de equação do segundo grau mais complexo, onde precisaremos simplificar as raízes.

Resolva a seguinte equação: x² + 6x + 7 = 0

Vamos descrever os coeficientes:

• a = 1
• b = 6
• c = 7

Calculando o Δ: Δ = b² – 4ac:

• Δ = 6² – 4 . 1 . 7 = 36 – 28 = 8

Segundo passo é substituir os valores na expressão:

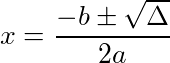
Para x₁, temos: 

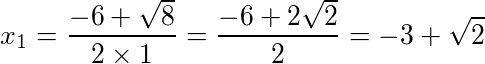
Para x₂, temos:

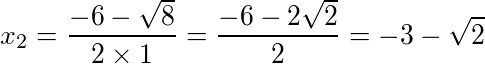
Essa é uma resposta mais complexa, pois tivemos que simplificar a raiz. Após a simplificação, dividimos os valores no numerador por 2. Esse processo de simplificar raiz pode ser estudado em radiciação.

• Responda os exercícios propostos, com gabarito.

Resolução de uma equação do segundo grau incompleta

Equações do segundo grau do tipo ax² + bx = 0 e ax² + c = 0, com a ≠ 0, são chamadas de equações incompletas, pois não possuem todos os parâmetros como uma equação completa.

Uma equação incompleta pode também ser resolvida utilizando a fórmula de Bhaskara, da mesma forma que resolvemos uma equação completa, caso o aluno entenda ser mais fácil usar a fórmula.

Dessa forma, temos que considerar c = 0 no primeiro caso e b = 0 no segundo caso.

Vamos aqui mostrar uma maneira mais eficiente e mais rápida de resolver uma equação incompleta. Vamos ver:

Considerem as equações abaixo:

• 3x² – 2x = 0
• x² + x = 0
• 8x² + 6x = 0

As equações acima são da forma ax² + bx = 0, com a ≠ 0.

Todas as equações que não possuem o termo independente c, como as equações acima, ou seja, c = 0, admite x = 0 como solução da equação.

Como todos os termos dependem da variável x, e x é nulo, os termos também serão anulados. Isso vale para qualquer equação independente do grau.

Encontramos, assim, uma das raízes da equação. O zero (0) é uma das soluções das equações acima. Para achar a outra raiz vamos fatorar o primeiro membro da equação:

Dividimos os dois lados por x.

Dessa forma, o conjunto solução para equações do tipo ax² + bx = 0 é dado por:

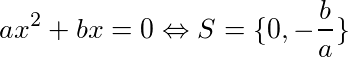
Agora veja como resolver as equações dadas no exemplo acima utilizando esta fórmula.

3x² – 2x = 0:

• a = 3
• b = -2

Assim, uma solução é 0, a outra é -b/a = -(-2)/3 = ²⁄₃

Logo: S = {0, ²⁄₃}

x² + x = 0:

• a = 1
• b = 1

Solução é: S = {0, -1}, substituímos direto.

8x² + 6x = 0:

• a = 8
• b = 6

Solução: S = {0, –³⁄₄}; -b/a = –⁶⁄₈ = –³⁄₄

Perceba que sabendo disso resolvemos rapidamente sem precisar fazer todos os passos da fórmula de Bhaskara. Em uma prova esse procedimento pode economizar tempo.

Para equações do tipo ax² + c = 0, com a ≠ 0, é similar. Mas neste caso x = 0 não é solução da equação. Vamos então encontrar uma fórmula que resolva equações incompletas, com b = 0.

Fatorando ax² + c = 0, temos:

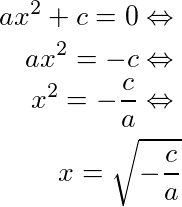
Portanto, para equação do segundo grau incompleta, do tipo ax² + c = 0, o conjunto solução é:

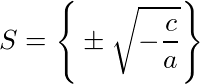
Essa fórmula encontra as raízes da equação se a e c tiverem sinais diferentes.

E S = Ø, se a e c tiverem o mesmo sinal, para x ∈ R.

Exemplo:

Considerem as equações incompletas abaixo:

x² – 2 = 0:

• a = 1
• c = -2

Solução:

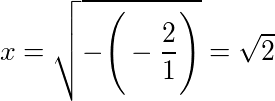
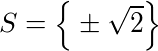
2x² + 1 = 0:

• a = 2
• c = 1

Solução:

S = Ø, pois a e c tem o mesmo sinal.

Portanto, caso o aluno saiba estas fórmulas para achar a solução para as equações incompletas de grau 2, o processo de resolução torna-se mais eficiente e rápido.

Não é necessário decorar, entenda o processo de fatoração que fizemos acima.

Veja uma nova forma de encontrar as raízes de uma equação do segundo grau sem utilizar a fórmula de Bháskara, através da soma e produto.

Exercícios

Acesse e resolva os exercícios clicando no link abaixo:

• Exercícios propostos com gabarito

Bons estudos!

Leia também

• Equação do 1º grau
• Porcentagem
• Tabuada