Soma e produto é uma técnica que podemos utilizar para encontrar as raízes de uma equação do segundo grau sem utilizar a fórmula de Bhaskara.
Uma equação do segundo grau possui a seguinte forma:
- ax² + bx + c = 0, com a, b e c ∈ R e a ≠ 0.
Onde:
- a: coeficiente principal;
- b: coeficiente secundário;
- c: termo independente.
Quando resolvemos uma equação do segundo grau e utilizamos a fórmula de Bhaskara, podemos chegar nas seguintes possibilidades.
- ∆ > 0: a equação possui duas raízes reais e distintas.
- ∆ = 0: uma única raiz real e distinta.
- ∆ < 0: nenhuma raiz real.
Se a equação possui raízes reais, podemos aplicar o seguinte método prático para encontrá-las:
- Soma das raízes: (x1 + x2)
- Produto das raízes: (x1 * x2)
Vamos aplicar o método acima para chegar a uma fórmula que possamos encontrar as raízes da equação, para isso vamos fazer a soma e o produto das fórmulas abaixo:
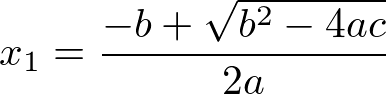
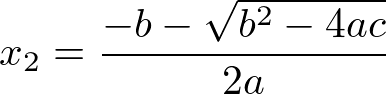
A partir dos dados acima, temos as seguintes expressões que podemos usar para encontrar as raízes de uma equação do segundo grau, através da soma e produto.
Soma:
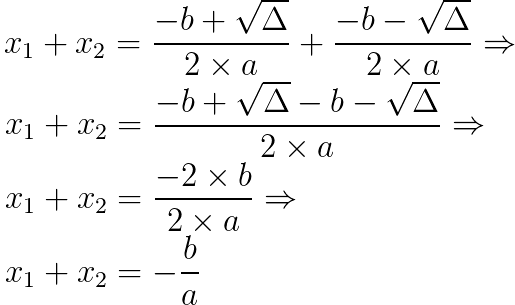
Produto:
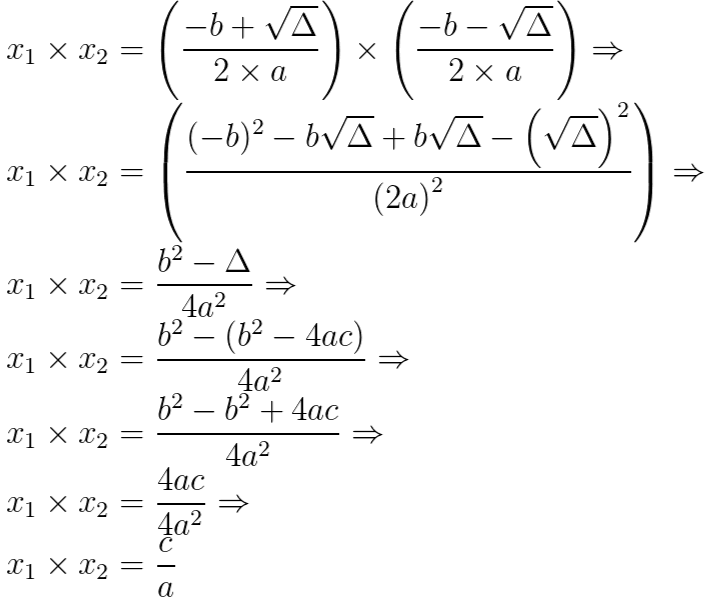
Sabendo que ∆ = b² – 4ac.
Com as fórmulas acima, podemos encontrar as raízes para uma equação do segundo grau. Vamos ver um exemplo prático como funciona.
Exemplo:
Seja a equação x² – 5x + 6 = 0, encontre as raízes que resolvem a equação. Veja o passo a passo sobre como fazer:
Passo 1: anotar os valores dos coeficientes da equação:
- a = 1;
- b = -5;
- c = 6;
Passo 2: aplicar as fórmulas que definimos acima:
Soma:
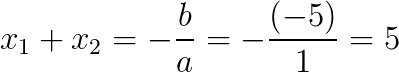
Produto:
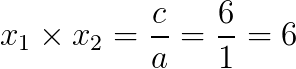
Passo 3: encontrar valores em que a soma (S) seja igual a 5 e o produto (P), seja igual a 6. É ideal começar pelos números candidatos ao produto, pois fica mais fácil.
Você deve perguntar: quais os números que eu multiplico e chego no resultado do produto?
Números candidatos para o produto:
- 2 . 3 = 6
- 1 . 6 = 6
- (-1) . (-6) = 6
Os números candidatos para a soma, dos números acima, é a primeira opção, pois:
- 2 + 3 = 5
Portanto, as raízes que formam o conjunto solução da equação: x² – 5x + 6 = 0 são 2 e 3.
Logo, S = {2, 3}.
Vamos conferir:
- 2: 2² – 5 . 2 + 6 = 4 – 10 + 6 = 0
- 3: 3² – 5 . 3 + 6 = 9 – 15 + 6 = 0
Legal, não é mesmo? Bem mais simples que utilizar a fórmula de Bhaskara. Devendo então anotar as fórmulas acima para da soma e do produto para x1 e x2.
Exercícios
Acesse os exercícios no link a seguir:



