A divisão é uma das quatro operações fundamentais da aritmética. Consiste em dividir dois números, o dividendo e o divisor, que produz dois resultados chamados quociente e resto.
Seu símbolo é o “÷”. No entanto, pode variar, por exemplo, no teclado do computador o símbolo adotado é a barra “/”, em outros casos, “:”.
A divisão é o ato de dividir em partes iguais para todos. O número que está sendo dividido em partes iguais é chamado dividendo; o número que indica em quantas vezes vamos dividir é chamado divisor; o resultado é o quociente; o que sobra é o resto.
Exemplos: 15 ÷ 2 = 7 (sobra 1, portanto tem-se resto 1)
Leia-se: “Quinze dividido por dois, igual a 7”
No exemplo acima, 15 é o dividendo, 2, o divisor, 7, o quociente (resultado), e 1 é o resto, ou seja, o que sobra como resto dessa divisão. O resto existe quando a divisão não é exata, ou seja, quando o resto é diferente de zero.
Condição de existência
Considere dois números naturais N e d tais que se dividirmos N por um divisor d, teremos um quociente q e um resto r. Essa regra deve obedecer as seguintes condições:
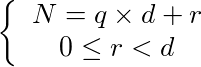
Essa condição nos diz que não existe um divisor igual a 0 (zero), pois pela segunda condição d > r, e r ≥ 0. Dessa forma, d = 0 não satisfaz a desigualdade 0 ≤ r < d.
Então, qualquer número N e d ≠ 0, temos que o quociente da divisão de N por d será o maior número natural q, desde que o produto q x d não seja maior que N. O resto dessa divisão é a diferença entre o dividendo N e o produto q x d.
Exemplo: 12 ÷ 3 = 4
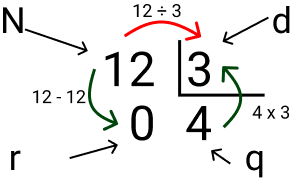
Com esse exemplo e a imagem podemos entender melhor. A divisão de 12 por 3 tem como quociente 4. O produto 4 x 3 não pode ser maior que 12. O resto é a diferença entre o produto (q x d) e N: (4 x 3) – 12.
Propriedades
Vamos estudar agora algumas propriedades importantes:
Não é comutativa
Dividir 2 ÷ 1 = 2 é diferente de dividir 1 ÷ 2 = 0,5, portanto a comutatividade não vale para a divisão.
Não é associativa
A associatividade não vale na divisão. Por exemplo, dividir (4 ÷ 2) ÷ 2 = 2 ÷ 2 = 1 tem resultado diferente de 4 ÷ (2 ÷ 2) = 4 ÷ 1 = 4. Lembrando que os parênteses têm prioridade na divisão, ou seja, devem ser resolvidos primeiros.
Fechamento
A propriedade de fechamento em que a divisão de dois números reais será um número real não satisfaz, pois a divisão por 0 (zero) não tem como resultado um número real.
Elemento neutro
O número 1 (um) é o elemento neutro na divisão, dividir um número por 1 (um) tem como resultado o próprio número. Faz todo sentido, por exemplo, dividir um pedaço de bolo com você mesmo, o pedaço será todo seu.
Anulação
O número 0 anula o resultado quando dividido por qualquer número real.
Casos particulares da divisão e multiplicação
Multiplicação
- Um número multiplicado por 1 (um) tem como resultado ele mesmo.
- Exemplo: 2 x 1 = 2
- Um número multiplicado por 0 (zero) tem como resultado o zero.
- Exemplo: 2 x 0 = 0
Divisão
- Um número dividido por 1 (um) tem como resultado ele mesmo.
- Exemplo: 2 ÷ 1 = 2
- Um número dividido por ele tem como resultado o número 1 (um).
- Exemplo: 2 ÷ 2 = 1
- Zero dividido por qualquer número tem como resultado o próprio zero.
- Exemplo: 0 ÷ 2 = 0
- Nenhum número real pode ser dividido por 0 (zero).
Regra dos sinais
A divisão de número naturais com sinais diferentes obedecem às seguintes regras:
- Sinais iguais: divide e o resultado fica positivo.
- Sinais diferentes: divide e o resultado fica negativo.
Jogo dos sinais
- + – = – (mais com menos é igual a menos)
- – + = – (menos com mais é igual a menos)
- + + = + (mais com mais é igual a mais)
- – – = + (menos com menos é igual a mais)
Exemplos:
- (-10) ÷ (+1) = -10 (Sinais diferentes: divide e o sinal fica negativo).
- (+10) ÷ (-1 ) = -10 (Sinais diferentes: divide e o sinal fica negativo).
- (-10) ÷ (-1) = +10 (Sinais iguais: divide e o sinal fica positivo).
- (+10) ÷ (+1) = +10 (Sinais iguais: divide e o sinal fica positivo).
Veja como resolver manualmente
Exemplos:
- 15 ÷ 2 = 7 (com resto 1).
- 14 ÷ 2 = 7 (divisão exata)
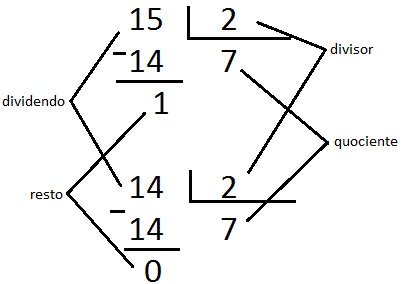
Quando dividimos manualmente dois números, devemos dividir o dividendo pelo divisor, o resultado dessa divisão é o quociente. Para encontrar o resto dessa divisão, basta multiplicar o quociente pelo divisor e subtrair pelo dividendo.
Exercícios propostos
Responda os exercícios de divisão propostos.
Veja mais…



