Inequação do 1º e 2º Grau: Entenda Com Exemplos

Inequação do 1º grau é diferente de uma equação do primeiro grau. Enquanto uma equação expressa uma igualdade, a inequação expressa uma desigualdade.

Definição de uma inequação do 1º grau

Chamamos de inequação do 1º grau uma desigualdade na variável x que pode ser reduzida em uma das formas: ax + b > 0 ou ax + b ≥ 0 ou ax + b < 0 ou ax + b ≤ 0, em que a, b ∈ R e a ≠ 0.

Na inequação utilizaremos os símbolos:

> (Leia-se: Maior que)
< (Leia-se: Menor que)
≥ (Leia-se: Maior ou igual)
≤ (Leia-se: Menor ou igual)

Esses sinais servem para comparar. A própria definição de inequação é clara, devemos descobrir números que satisfazem essa comparação.

Exemplo: x – 1 > 3

Qual o número que podemos substituir a incógnita x para que satisfaça essa inequação? É fácil perceber que qualquer valor maior que 4 é verdade.

Como resolver uma inequação do 1º grau?

Para resolver uma inequação do 1º grau, o que fazemos é determinar um conjunto com todos os valores para a variável x que torna a sentença verdadeira.

Propriedades da inequação do 1º grau

Resolvemos problemas de inequação isolando a variável x na sentença. Então as seguintes propriedades são utilizadas. Considerando x, y e a números reais:

x < y ⇔ x + a < y + a, ∀a ∈ R
x < y ⇔ ax < ay, se a > 0
x < y ⇔ ax > ay, se a < 0

Vejamos agora como resolvermos uma inequação. Também faremos uma representação gráfica para você poder entender melhor.

Exercícios resolvidos

Considere as seguintes inequações:

2x + 2 > 0
x – 2 < 0
5x – 10 ≥ 0
3x + 3 ≤ 0

Exemplo 1: 2x + 2 > 0

Para achar o conjunto solução desse problema, ou seja, quais valores podemos substituir em x tal que satisfaça esse problema.

2x + 2 > 0
2x > -2
x > –²⁄₂
x > -1

Dessa forma qualquer valor maior que -1 satisfaz o problema.

Analisando o gráfico acima temos que todos os valores maiores que -1 resolvem a inequação. No gráfico a bola sem preenchimento indica que somente valores maiores que -1, ou seja, a parte indicada pela parte em vermelho formam o conjunto solução que pode ser representado assim: S = {x ∈ R; x > -1}.

Exemplo 2: x – 2 < 0

x – 2 < 0
x < 2

Neste exemplo qualquer valor menor que 2 satisfaz a inequação.

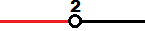
A parte vermelha do gráfico mostra que somente os valores menores que 2 resolvem a inequação. Dessa forma, o conjunto solução para esse problema é: S = {x ∈ R; x < 2}.

Exemplo 3: 5x – 10 ≥ 0

5x – 10 ≥ 0
5x ≥ 10
x ≥ ¹⁰⁄₅
x ≥ 2

Para este problema qualquer valor maior ou igual a 2 resolve o problema.

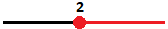
Esse gráfico é um pouco diferente do primeiro. Aqui temos uma representação com a bola no gráfico totalmente preenchida. Isso quer dizer que todos os valores maiores que 2, e também o número 2, fazem parte do conjunto solução desse problema. Assim: S = {x ∈ R; x ≥ 2}.

Exemplo 4: 3x + 3 ≤ 0

3x + 3 ≤ 0
3x ≤ -3
x ≤ –³⁄₃
x ≤ -1

Assim, qualquer valor menor ou igual a -1 satisfaz esse problema.

O gráfico mostra que todos os valores menores que -1, e também o -1, resolvem a inequação. Assim: S = {x ∈ R; x ≤ -1}.

Sistema de inequações do 1º grau

Assim como temos os sistemas lineares que envolvem equações do 1º grau, também temos os sistemas de inequações do 1º grau.

Considere o sistema com as seguintes inequações:

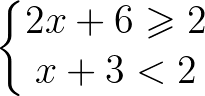
Inequação do 1º e 2º Grau: Entenda Com Exemplos

Para resolver esse sistema devemos resolver cada inequação separadamente, e depois analisar os conjuntos soluções encontrados para cada uma das desigualdades.

Então, vamos resolver o primeiro problema:

2x + 6 ≥ 2
2x ≥ 2 – 6
2x ≥ -4
x ≥ –⁴⁄₂
x ≥ -2

Portanto, para qualquer valor maior ou igual a -2 satisfaz essa inequação.

Agora vamos resolver o segundo problema:

x + 3 < 2
x < 2 – 3
x < -1

Portanto, neste problema temos que qualquer valor menor que -1 satisfaz o problema.

Então, temos o seguinte gráfico para o sistema:

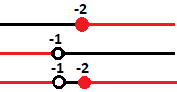
Em um sistema de inequações precisamos analisar e responder cada inequação separadamente e depois comparar os gráficos lado a lado para encontrar o conjunto solução que resolve as inequações do sistema.

Dessa forma, resolvemos o primeiro problema e encontramos que qualquer valor maior ou igual a -2 faz parte do conjunto solução e está representado pelo primeiro gráfico. Na segunda inequação encontramos que qualquer valor menor que -1 resolve o segundo problema, veja o gráfico do meio.

Mas para encontrar o conjunto solução do sistema devemos colocar os gráficos paralelamente na horizontal, construir um novo gráfico e analisar.

Assim, para esse sistema qualquer valor menor que -1 e qualquer valor maior ou igual a -2 resolve esse sistema, como pode ser visto no gráfico de baixo. Portanto, o conjunto solução do sistema é: S = {x ∈ R; x < -1 ou x ≥ -2}.

Inequação do 2º grau

Uma inequação do 2º grau é uma desigualdade parecida com uma equação do 2º grau, porém as inequações apresentam uma desigualdade, enquanto as equações uma igualdade entre os termos.

Definição de uma inequação do 2º grau

Chamamos de inequação do 2º grau uma desigualdade na variável x que apresenta um grau 2 e pode ser reduzida em uma das formas: ax² + bx + c > 0 ou ax² + bx + c ≥ 0 ou ax² + bx + c < 0 ou ax² + bx + c ≤ 0, com a, b, c ∈ R e a ≠ 0.

Exemplos:

2x² + 2x + 2 ≤ 0
x² + x – 1 < 0
3x² – 2x + 2 ≥ 0
5x² – x + 1 > 0

Como resolver uma inequação do 2º grau?

Resolvemos uma inequação encontrando um conjunto solução com todos os valores que se substituído na variável x tornam a sentença verdadeira.

Método de resolução

Considerando y = f(x) = ax² + bx + c, com a ≠ 0, analisaremos a variação de sinais nessa função para conseguirmos chegar a solução desta maneira:

Vamos encontrar as raízes reais para a função f assinalando os valores no eixo x das abscissas;
Desenhar o gráfico que representa a função f definida por uma parábola passando pelos valores das raízes do item anterior;
Marcar no eixo x os valores que satisfazem a sentença. Caso a função não admitir raízes reais, então f(x) > 0 ∀x ∈ R, para a > 0 ou f(x) < 0 ∀x ∈ R para a < 0.

Exercício resolvido

1) Encontre o conjunto solução para a inequação: x² + x – 2 ≤ 0.

Para resolver uma inequação do 2º grau devemos seguir o mesmo método usado para resolver uma equação do 2º grau, usando a fórmula de Bhaskara.

Então, para o problema acima vamos aplicar a fórmula:

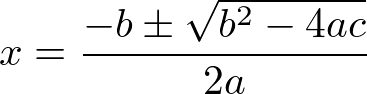
Os coeficientes a, b e c são:

a = 1
b = 1
c = -2

Vamos resolver primeiramente o discriminante Δ (delta): Δ = b² – 4ac

Δ = b² – 4ac = 1² – 4.1.(-2) = 1 + 8 = 9

Agora vamos utilizar a expressão abaixo para encontrar as raízes reais que resolvem o problema:

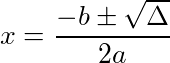
Substituindo os valores dos coeficientes acima, temos:

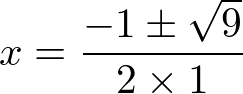
Perceba que temos um mais ou menos alí entre -1 e a raiz. Então vamos ter que calcular separadamente para facilitar o entendimento. Vamos chamar de x₁ para + e x₂ para –, então:

Para x₁, temos:

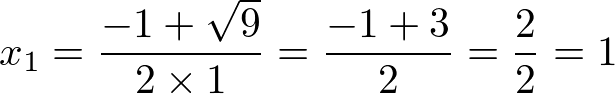
Para x₂, temos:

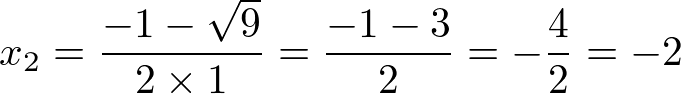
Logo, o conjunto solução para a inequação do exemplo é: S = {x ∈ R; -2 ≤ x ≤ 1}

Agora precisamos desenhar o gráfico para a inequação do exemplo, esboçando o intervalo definido pelas raízes que forma o conjunto solução para o problema proposto.

Gráfico de uma inequação do 2º grau

O gráfico de uma inequação do 2º grau é uma função, então para a inequação do exemplo temos que: f(x) = x² + x – 2. As raízes para f são as raízes que encontramos usando a fórmula de Bhaskara, assim x₁ = -2 e x₂ = 1.

Como o coeficiente é a > 0 temos que a função tem a parábola com a concavidade voltada para cima.

Então o gráfico para f é:

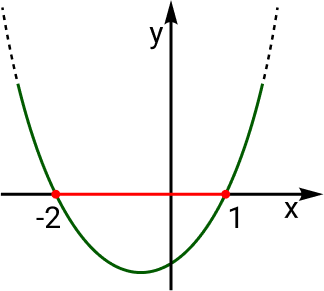
Logo, para -2 ≤ x ≤ 1, temos que f ≤ 0.

Exercícios

Veja os exercícios no link abaixo:

Exercícios sobre inequações

Bons estudos!

Veja mais…