Responda os exercícios a seguir sobre inequações do 1º e 2º grau para ajudar no entendimento do assunto, confira as respostas após respondê-los.
1) Resolva a inequação em R: 2x + 2 ≤ x + 1
Ver resposta
2x + 2 ≤ x + 1 ⇒
2x – x ≤ – 2 + 1 ⇒
x ≤ – 1
S = {x ∈ R | x ≤ – 1}
2) Determine o conjunto solução em R para a inequação 3x + 4 > 0
Ver resposta
3x + 4 > 0 ⇒
3x > – 4 ⇒
x > – 4/3
S = {x ∈ R | x > – 4/3}
3) Resolva em R a inequação do 2º grau (x + 1)(x + 3) ≥ 0, esboce o gráfico.
Ver resposta
A desigualdade (x + 1)(x + 3) ≥ 0 é equivalente a x² + 4x + 3 ≥ 0, assim:
Os coeficientes são: a = 1, b = 4 e c = 3
Utilizando Bhaskara, temos que:
Δ = 4² – 4 . 1 . 3 = 16 – 12 = 4
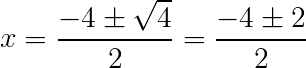
x = -2/2 = -1 ou x = – 6/2 = -3
Portanto, S = {x ∈ R | x ≤ -3 ou x ≥ -1}
O gráfico para f(x) = x² + 4x + 3 é:
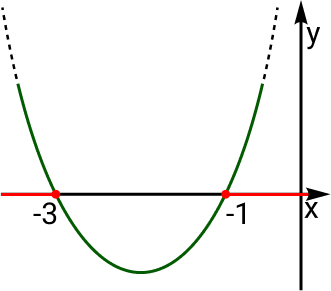
Logo, para x ≤ -3 ou x ≥ -1, f ≥ 0
4) Determine o conjunto solução do sistema a seguir:
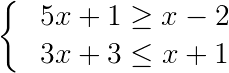
Ver resposta
Primeiro devemos responder separadamente às desigualdades:
5x + 1 ≥ x – 2 ⇒
5x – x ≥ -1 – 2 ⇒
4x ≥ – 3 ⇒
x ≥ – 3/4
3x + 3 ≤ x + 1 ⇒
3x – x ≤ – 3 + 1 ⇒
2x ≤ – 2 ⇒
x ≤ – 2/2 ⇒
x ≤ – 1
Assim, temos x ≥ – 3/4 ou x ≤ – 1 que não satisfaz o problema e o sistema não possui solução em R.
Portanto, o conjunto solução para o sistema é: S = {Ø}
5) Quais os valores reais que podemos atribuir a x que tornam a desigualdade x – 20 < 2x + 6 verdadeira?
Ver resposta
Resolvendo, temos:
x – 20 < 2x + 6 ⇒
x – 2x < 20 + 6 ⇒
– x < 26 ⇒ (multiplica por -1, inverte o sinal da desigualdade)
x > -26
Portanto, o conjunto solução é: S = {x ∈ R | x > – 26}


