Sistemas lineares são um conjunto de equações lineares, com m equações e n incógnitas. A solução de um sistema linear é a solução de todas as equações do sistema.
Existem muitas maneiras de resolvermos um sistema de equações lineares ou sistemas lineares, como quiser chama-los. Aqui, vamos aprender a regra mais fácil, pois o intuito do site é facilitar a vida do estudante e não complicar.
Equação linear
Antes disso, porém, vamos entender o que é uma equação linear para depois estudarmos e entendermos sistemas lineares.
Uma equação linear é qualquer equação da forma: a1x1 + a2x2 + a3x3 + … + anxn = b onde a1, a2, a3, …, an são números reais e b é um termo independente. Caso b = 0, a equação é chamada linear homogênea.
Exemplo: 2x1 + 5x2 – x3 + 3x4 = -2
Sistema linear
Um sistema linear é formado por um conjunto de equações lineares e tem a seguinte forma:

Cuja solução pertence aos números reais e o conjunto solução do sistema é resolve todas as equações lineares do sistema.
Exemplo:

Solução de um sistema linear
O conjunto ordenado dos números (a1, a2, a3, …, an) é solução do sistema linear nas incógnitas x1, x2, x3, …, xn, para x1 = a1, x2 = a2, …, xn = an, então as equações do sistema são verdadeiras.
Matriz associada a um sistema linear
Podemos associar a um sistema linear algumas matrizes, onde os seus coeficientes ocuparão linhas e colunas da matriz.
Seja o sistema:
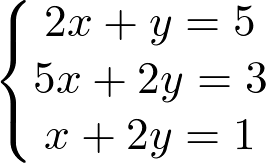
Matriz incompleta: formada apenas pelos coeficientes do sistema.
Exemplo:
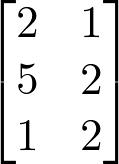
Matriz completa: formada pelos coeficientes do sistema e os temos independentes.
Exemplo:
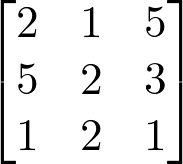
Equação matricial dos sistemas lineares
A equação matricial de um sistema linear é formada pelos coeficientes das equações, pelas variáveis e pelos termos independentes após a igualdade.
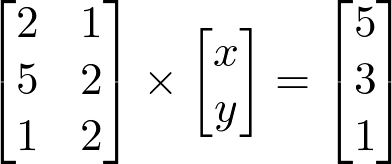
A solução para o sistema que forma essa equação linear é encontrar valores para as variáveis x e y.
Classificação de sistemas lineares
Os sistemas lineares são classificados conforme o número de soluções apresentados por ele. Assim, os sistemas lineares podem ser classificados como:
- SPD — Sistema Possível e Determinado — possui uma única solução.
- SPI — Sistema Possível e Indeterminado — possui infinitas soluções.
- SI — Sistema Impossível — não possui solução.
O fluxograma a seguir mostra como as soluções dos sistemas são divididas:
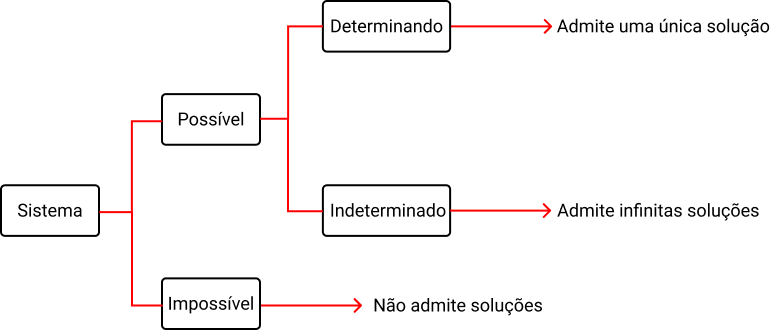
Como saber se um sistema linear tem solução?
Para sabermos se um sistema possui solução, basta calcularmos o determinante da matriz associada ao sistema, assim:
- SPD (Sistema Possível e Determinado): se o determinante diferir de zero;
- SPI (Sistema Possível e Indeterminado) se o determinante for igual a zero;
- SI (Sistema Impossível) se o determinante principal for igual a zero e o determinante secundário diferir de zero.
Como resolver sistemas lineares?
Existem diferentes formas para a resolução de sistemas, no entanto, vamos mostrar apenas duas: Regra de Cramer e Escalonamento.
Regra de Cramer
A Regra de Cramer é utilizada na resolução de sistemas SPD (sistemas possíveis e determinados). Tem os seguintes passos:
Para calcular o determinante principal, formamos uma matriz com os coeficientes das
variáveis;

Para calcular os determinantes secundários, substituímos as colunas das variáveis pela coluna do termo independente;

Obtemos as soluções para o sistema pela fórmula:
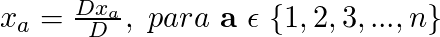
Exemplo:
Considere o sistema:

Então, o determinante principal é:
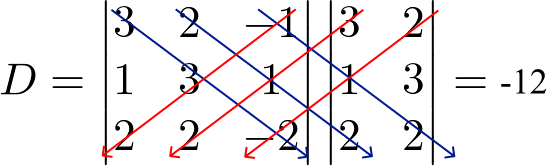
[3 . 3 . (-2)] + [2 . 1 . 2] + [(-1) . 1 . 2] – [2 . 1 . (-2)] – [3 . 1 . 2] – [(-1) . 3 . 2] = -18 + 4 – 2 + 4 – 6 + 6 = -12
Os determinantes secundários são:
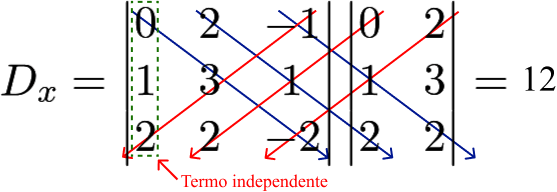
[0 . 3 . (-2)] + [2 . 1 . 2] + [(-1) . 1 . 2] – [2 . 1 . (-2)] – [0 . 1 . 2] – [(-1) . 3 . 2] = 0 + 4 – 2 + 4 – 0 + 6 = 12
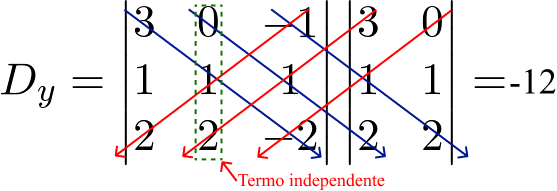
[3 . 1 . (-2)] + [0 . 1 . 2] + [(-1) . 1 . 2] – [0 . 1 . (-2)] – [3 . 1 . 2] – [(-1) . 1 . 2] = – 6 + 0 – 2 – 0 – 6 + 2 = -12
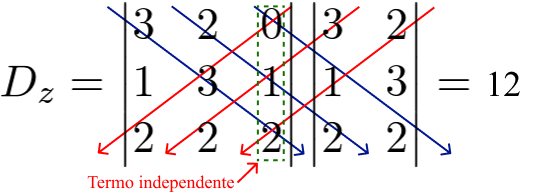
[3 . 3 . 2] + [2 . 1 . 2] + [0 . 1 . 2] – [2 . 1 . 2] – [3 . 1 . 2] – [0 . 3 . 2] = 18 + 4 + 0 – 4 – 6 – 0 = 12
Para calcular o determinante utilizamos a Regra de Sarrus para matrizes quadradas de ordem 3.
Logo,
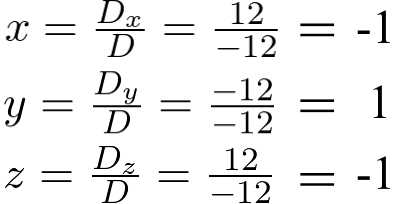
A solução do sistema é (-1, 1, -1).
Escalonamento de sistemas lineares
Escalonar um sistema é uma forma de resolvê-lo transformando o sistema em outro equivalente que possua uma resolução mais fácil. Os passos para escalonar um sistema são:
- Somar ou subtrair uma equação pela outra;
- Multiplicar uma das equações inteira por um número real diferente de zero;
- Trocar duas equações de posições entre si;
- Multiplicar um das equações por um número real e somá-la ou subtraí-la a outra;
- Dividir uma equação inteira por um número real diferente de zero.
Seguindo esses passos podemos escalonar um sistema e encontrar os valores para as variáveis que resolvem o sistema. Esta categoria de escalonamento é chamado forma escalonada ou de redução à forma escada, pois quando vamos escalonando um sistema, uma “escada” vai se formando.
Observação: os passos indicados acima não precisam ser executados necessariamente nessa ordem, nem executar todos os passos. É apenas um norte a ser seguido.
Exemplo:
Considere o sistema abaixo:

Para fazermos o escalonamento devemos transformar o sistema acima em uma matriz. Assim, pegamos os valores dos coeficientes e do termo independente após a igualdade.

Com a matriz montada, o primeiro passo é fazer uma operação (adição, subtração, multiplicação ou divisão) que anula pelo menos um elemento da matriz.
Ao analisar a matriz, percebe-se que se subtrairmos a linha 2 com a linha 1, anulamos um elemento. O resultado dessa subtração é colocado na linha 2, como mostra L’2 do lado direito da matriz abaixo:
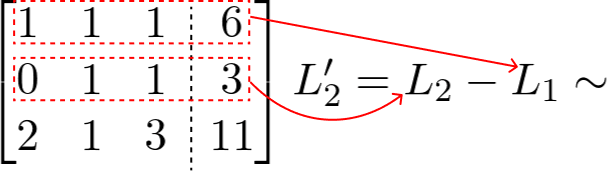
Próximo passo, anulamos mais um elemento subtraindo a linha 3 pelo dobro da linha 1, colocando o resultado na linha 3. Veja:
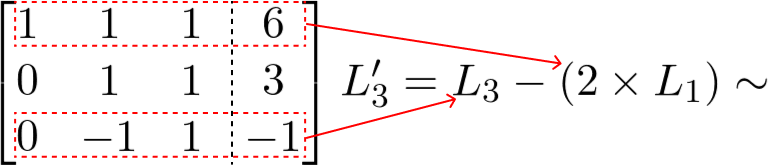
Agora, se somarmos a linha 2 com a linha 3, anulamos mais um elemento.
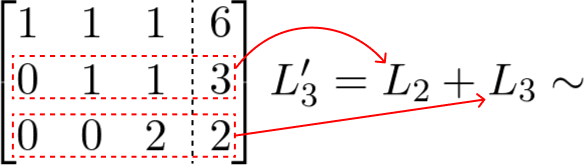
A diagonal principal não pode ser nula, então temos que transformar o número 2 em 1, para isso basta dividirmos a linha 3 por 2. Veja:
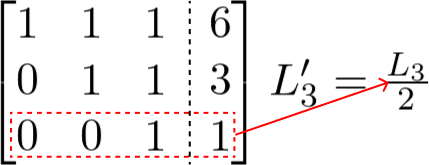
Neste passo já temos a forma escalonada, aqui já é possível encontrar os valores das variáveis x, y e z. Fazendo a substituição nas equações do sistema, pois já sabemos que a variável z é igual a 1.

Vamos prosseguir para ver o processo até o final. O intuito agora é anularmos os elementos acima da diagonal principal.
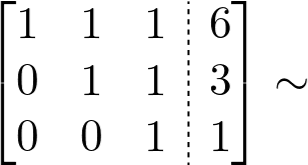
Perceba que se subtrairmos a linha 2 com a linha 3, anulamos um elemento. Veja:
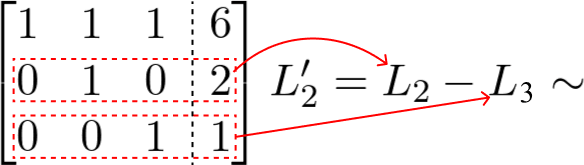
Continuando, vamos anular mais um elemento que não está na diagonal principal, para isso devemos subtrair a linha 1 com a linha 3.
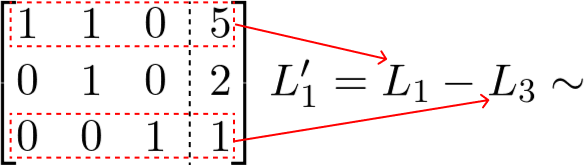
Por fim, vamos anular o último elemento que não está na diagonal principal. Então subtraímos a linha 1 pela linha 2.
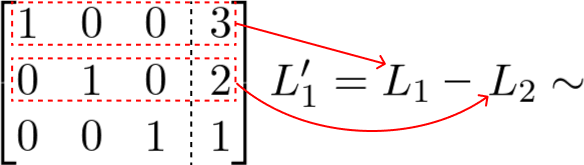
Portanto, essa é a matriz escalonada. Os valores encontrados no termo independente são os valores que atribuídos as variáveis x, y e z formam o conjunto solução do sistema. A matriz abaixo é a escalonação reduzida à forma escada.

Montando o sistema novamente, temos um sistema equivalente fácil de resolver:
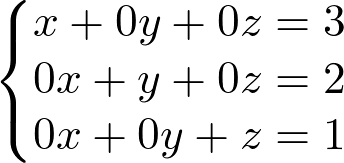
Assim, x = 3, y = 2 e z = 1.
Exercícios
Para ver os exercícios propostos, acesse o link abaixo:
Bons estudos!
Leia também…



