Encontrar uma matriz inversa é uma forma de resolvermos equações matriciais que têm a forma A . X = B.
Como não é possível realizar a operação de divisão com matrizes, os matemáticos criaram técnicas de forma que possamos fazer a inversão de uma matriz da mesma forma que fazemos para encontrar o inverso de um número real.
A multiplicação de uma matriz qualquer por sua inversa resulta na matriz identidade de mesma ordem. A matriz identidade é uma matriz em que os elementos da sua diagonal principal são todos 1 (um) e o restante dos elementos são 0 (zeros). Com notação In.
Exemplo:

Definição de Matriz Inversa
Seja a matriz Anxn, quadrada, ou seja, mesma quantidade de linhas e colunas, a matriz inversa para A é dada por A-1nxn, tal que:
Anxn . A-1nxn = A-1nxn . Anxn = Inxn
Onde Inxn é uma matriz identidade de ordem n, também quadrada.
Observação:
É importante lembrar que uma matriz pode não ser inversível. Se uma matriz A possuir inversa, dizemos que A é inversível, sendo que a sua inversa é uma matriz única. Se A não for inversível, dizemos que A é uma matriz singular.
Como saber se uma matriz é inversível?
Para sabermos se uma matriz é inversível precisamos encontrar o seu determinante. Se o determinante de uma matriz for diferente de zero, então a matriz é inversível. Caso contrário ela não possui uma matriz inversa.
Dessa forma, podemos concluir que somente uma matriz quadrada possui inversa, já que somente podemos calcular o determinante de uma matriz quadrada. Uma matriz quadrada é uma matriz que possui a mesma quantidade de linhas e colunas.
Como fazer a inversa de uma matriz?
Para calcularmos a inversa de uma matriz, usamos o método de resolução por sistemas lineares. Como vimos na definição acima, a multiplicação de uma matriz pela sua inversa tem como resultado uma matriz identidade.
A partir disso podemos criar um sistema de equações lineares e calcular a inversa da matriz em questão.
Exemplo:
Seja A uma matriz quadrada de ordem n, a inversa de A é A-1, pela definição, se A é inversível então A . A-1 = In.
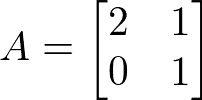
Primeiramente para sabermos se A é inversível temos que calcular seu determinante. Então:
det (A) = 2 . 1 – 1 . 0 = 2 – 0 = 2
Como o determinante de A é diferente de zero, então A possui inversa e podemos continuar.
Não sabe como calcular o determinante de uma matriz? Veja como calcular aqui.
Por A . A-1 = In temos que os elementos de A e da identidade são conhecidos, mas os elementos de A-1 não sabemos quais são, então vamos definir as variáveis x, y, z e w como seus elementos. Assim:
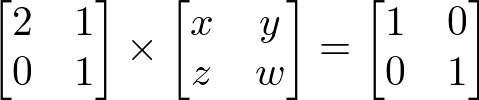
Veja que substituímos A . A-1 = In pelas matrizes em questão.
Próximo passo é realizar a multiplicação dos elementos de A pelos elementos de A-1. Então:
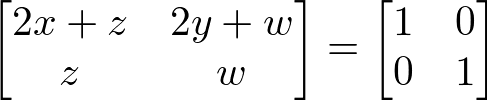
Agora podemos montar um sistema de equações lineares de forma que possamos encontrar os valores para x, y, z e w. Vamos fazer a correspondência de cada elemento da matriz à esquerda corresponda com a matriz identidade à direita. Dessa forma, teremos dois sistemas:
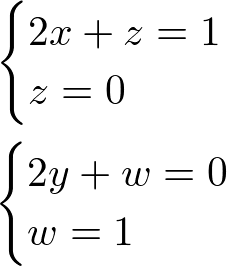
É importante que as variáveis iguais fiquem no mesmo sistema, como w e z nos sistemas acima.
A partir dos sistemas montados, agora é só resolver. Assim:
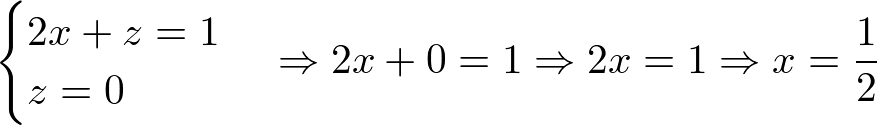
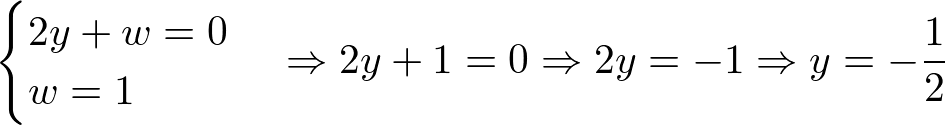
Com os valores de x, y, z e w encontrados, então encontramos a inversa de A. Portanto,
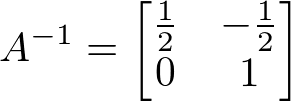
Verificando se A-1 é mesmo a inversa de A
Pela definição temos que A . A-1 = In. Então vamos multiplicar A por A-1 e ver se encontremos a matriz identidade.

Como encontramos uma matriz identidade, então A-1 é a inversa de A.
Vamos ver um exemplo de uma matriz A de ordem 3.
Considere a matriz A, a seguir, calcule a sua inversa A-1:
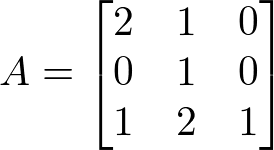
Primeiro devemos verificar se A é inversível. Para matrizes quadradas de ordem 3 calculamos o determinante utilizando a regra de Sarrus.
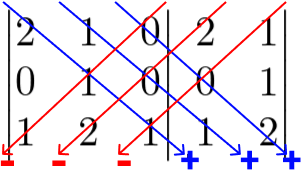
Então, det (A) = 2 . 1 . 1 + 1 . 0 . 1 + 0 . 0 . 2 – 0 . 1 . 1 – 2 . 0 . 2 – 1 . 0 . 1 = 2. Como det (A) ≠ 0, A é inversível.
Usando a definição: A . A-1 = In. Vamos substituir as matrizes na fórmula.

Multiplicando A por A-1 temos:
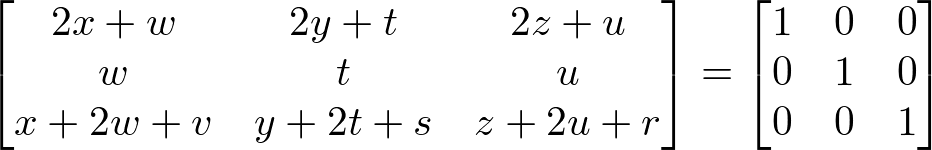
Fazendo a correspondência entre os elementos do lado esquerdo com os elementos da matriz identidade do lado direito, temos os seguintes sistemas:
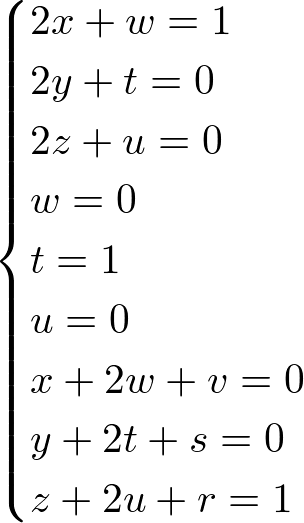
Resolvendo o sistema acima, temos:
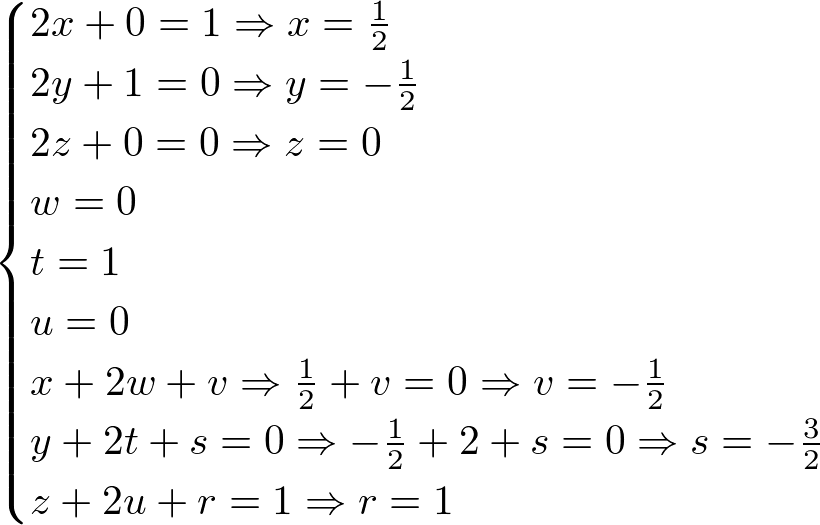
Logo,

Propriedades
Considere A e B matrizes quadrada de mesma ordem, então:
- (A-1)-1 = A: a matriz inversa da inversa de A é a própria matriz A.
- (At)-1 = (A-1)t: inversa da transposta de A é igual à transposta da matriz inversa de A.
- (A . B)-1 = B-1 . A-1: inversa do produto de A por B é igual ao produto das matrizes inversa de B pela inversa de A.
Exercícios
Responda os exercícios propostos, acesse o link a seguir:
Bons estudos!
Leia também…



