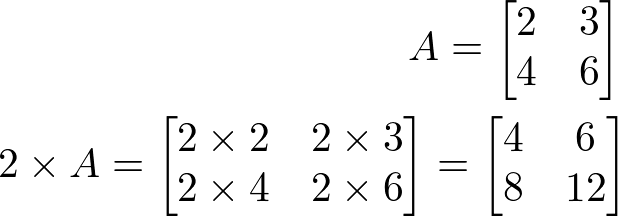Multiplicação de Matrizes: Aprenda a Fazer!

A multiplicação de matrizes é diferente da adição e subtração de matrizes.

Enquanto que na adição e subtração nós fazemos as operações entre os elementos correspondentes, na multiplicação entre duas matrizes nós devemos multiplicar os elementos das linhas da primeira matriz com os elementos contidos nas colunas da segunda matriz.

Índice do Artigo

Definição

Sejam as matrizes A e B, o produto entre A e B, escrevemos A x B ou A . B, só é possível se o número de colunas da matriz A for igual ao número de linhas da matriz B. Então:

Com isso, o produto entre A e B, produz como resultado uma matriz C, em que C é obtida pela multiplicação dos elementos das linhas de A pelos elementos das colunas de B. Então:

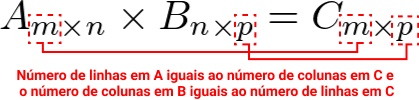
Multiplicação de matrizes passo a passo

Para entendermos melhor a definição acima vamos aplicá-la em um exemplo e ver como funciona passo a passo:

Exemplo:

Sejam as matrizes A e B abaixo:

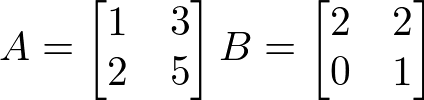
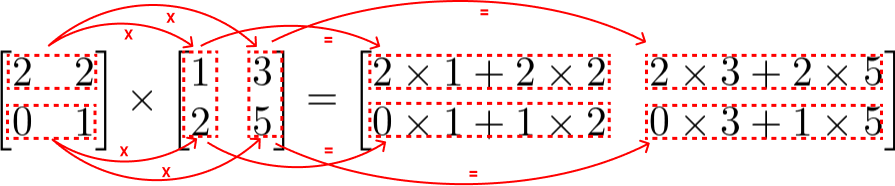
Agora vamos fazer o passo a passo da multiplicação entre essas duas matrizes:

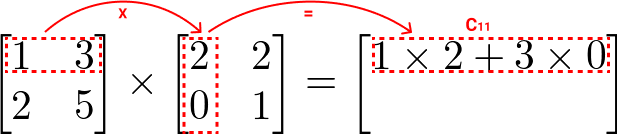
Multiplicamos primeiro a 1ª linha de A com a 1ª coluna de B:

Depois multiplicamos a 1ª linha de A e com a 2ª coluna de B:

Continuando, multiplicamos a 2ª linha de A com a 1ª coluna de B:

Por fim, multiplicamos a 2ª linha de A com a 2ª coluna de B:

Então temos que:

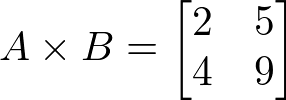
Para a multiplicação de matrizes a propriedade comutativa não vale, isto é, A . B ≠ B . A

Vamos multiplicar o exemplo anterior e verificar que A . B produz um resultado diferente do produto B . A.

Portanto, temos um resultado diferente de A . B:

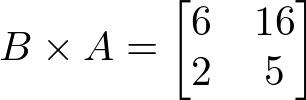
Assim, concluímos que a propriedade comutativa não vale para a multiplicação de matrizes.

Agora vamos ver um exemplo em que a ordem das matrizes seja diferente.

Exemplo:

Considere as matrizes A de ordem 2×2 e B de ordem 2×3 a seguir;

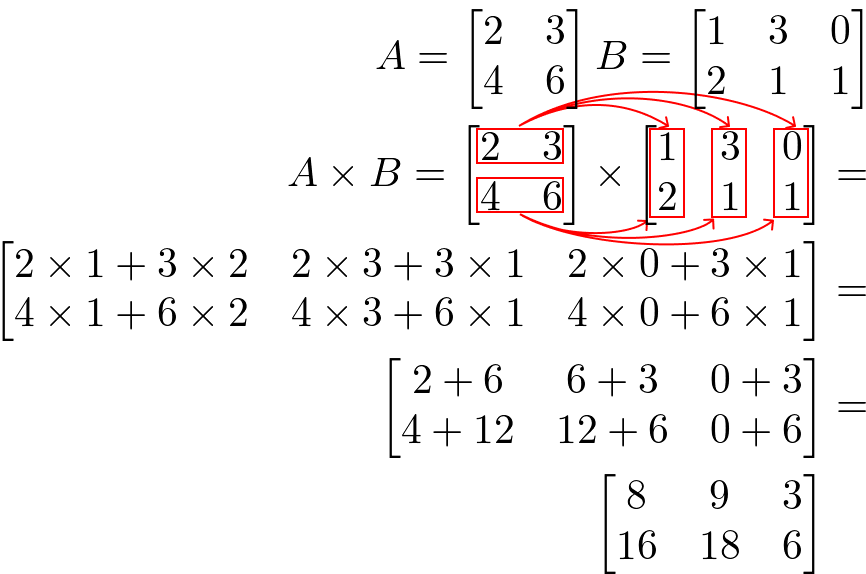
Então, a multiplicação entre essas duas matrizes só é possível porque o número de colunas de A é igual ao número de linhas em B, como mostra a definição.

Propriedades da multiplicação de matrizes

Sejam as matrizes A, B e C e a um número real qualquer, se as operações abaixo forem possíveis, temos que:

1. Associativa: A . (B . C) = (A . B) . C
2. Distributiva à esquerda: A . (B + C) = A . B + A . C
3. Distributiva à direita: (A + B) . C = A . C + B . C
4. Elemento neutro: A_mxn . I_n = I_n . A_mxn = A_mxn
5. (a . A) . B = A . (a . B) = a . (A . B)
6. (A . B)^t = B^t . A^t

Multiplicação de um número real por uma matriz

Seja a um número real qualquer e A uma matriz de ordem mxn. O produto a por A, escrevemos a . A, temos como resultado uma matriz B de ordem mxn, em que B é o resultado do produto entre a por todos os elementos de A.

Exemplo:

Encontrou algum erro? Nos avise clicando aqui