Matrizes: Definições, Operações e Determinantes

Matrizes são organizações de informações numéricas em uma tabela retangular formada por linhas e colunas.

Essa organização em uma tabela facilita que se possa efetuar vários cálculos simultâneos com as informações contidas na matriz.

Definição de matrizes

Toda matriz tem o formato m x n (leia-se: m por n, com m e n ∈ N*), onde m é o número de linhas e n o número de colunas.

Representação de matrizes

Existem diversas maneiras de representarmos matrizes, veja quais são:

• Colchetes: [ ]
• Parênteses: ( )
• Barras Simples: | |
• Barras Duplas: || ||

Essas são as representações mais comuns que encontramos na literatura.

Exemplos:

Elementos de uma matriz

Seja a matriz genérica A_mxn, isto é, m representa as linhas e n o número de colunas. Então, temos:

Dessa forma, os elementos da matriz A são indicados por a_ij, onde o i representa o índice da linha e j representa o índice da coluna para o elemento em questão. Assim, para localizarmos um elemento na coluna, procuramos o número da linha e da coluna, esses números são os índices i e j.

Pela imagem acima, veja que as linhas são numeradas de cima para baixo, enquanto as colunas são numeradas da esquerda para a direita.

Exemplos:

• a₁₁ representa o elemento da linha 1 e coluna 1.
• a₃₂ representa o elemento da linha 3 e coluna 2.
• a₂₂ representa o elemento da linha 2 e coluna 2.
• a_mn representa o elemento da linha m e coluna n.

Seja a matriz

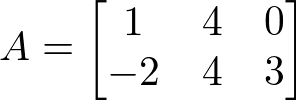
assim:

• a₁₁ representa o elemento 1.
• a₁₂ representa o elemento 4.
• a₁₃ representa o elemento 0.
• a₂₁ representa o elemento -2.
• a₂₂ representa o elemento 4.
• a₂₃ representa o elemento 3.

Uma matriz também pode ser representada por uma forma abreviada de forma que possamos escrevê-la facilmente.

Exemplo:

Considere a matriz M = [a_ij]_2×3, tal que a_ij = i + j. Escreva a matriz M.

Primeiramente vamos verificar as informações passadas. Observe que teremos uma matriz retangular, com 2 linhas e 3 colunas. Os elementos da matriz é a soma dos índices (posição) das linhas e colunas. Assim:

Escrevendo os elementos:

• a₁₁ = 1 + 1 = 2.
• a₁₂ = 1 + 2 = 3.
• a₁₃ = 1 + 3 = 4.
• a₂₁ = 2 + 1 = 3.
• a₂₂ = 2 + 2 = 4.
• a₂₃ = 2 + 3 = 5.

Então a matriz M é:

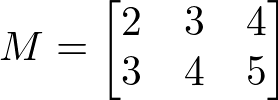
Matrizes Especiais

Vamos conhecer agora alguns tipos de matrizes especiais que é muito importante saber.

Matriz Linha

É uma matriz que possui somente uma linha (ordem 1 x n)

Exemplo:

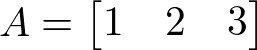
Matriz Coluna

É uma matriz que possui uma única coluna (ordem m x 1)

Exemplo:

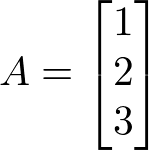
Matriz Nula

É uma matriz que possui todos os seus elementos iguais a zero.

Exemplo:

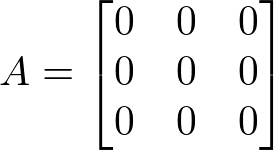
Matriz Quadrada

É uma matriz em que o número de colunas é igual ao número de linhas. Sendo que uma matriz quadrada de ordem mxn podemos dizer que ela tem ordem n

Exemplo:

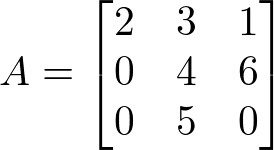
Essa é uma matriz quadrada de ordem 3 x 3, ou simplesmente de ordem 3. Numa matriz quadrada de ordem n, temos que os elementos a_ij com i = j formam a diagonal principal, enquanto os elementos i + j = n + 1, formam a diagonal secundária. Veja:

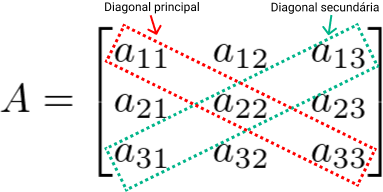
Elementos da diagonal principal da matriz A.

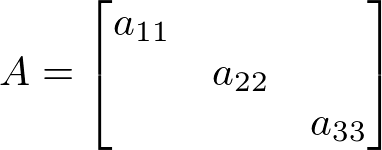
Elementos da diagonal secundária da matriz A.

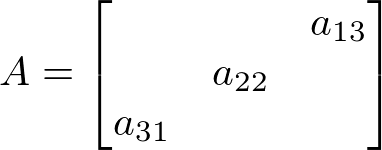
Obervação:

Quando uma matriz não é quadrada chamamo-la matriz retangular.

Matriz Diagonal

É uma matriz quadrada onde todos os elementos que não pertencem à diagonal principal são nulos.

Exemplo:

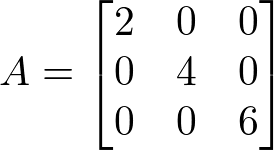
Matriz Identidade

É uma matriz quadrada em que todos os elementos que não pertencem à diagonal principal são nulos e os elementos da diagonal principal são 1. É representada por I_n, matriz quadrada de ordem n.

Exemplos

I₂ = Matriz identidade de ondem 2

I₃ = Matriz identidade de ondem 3

Leia mais sobre matriz identidade.

Matriz Oposta

É uma matriz obtida trocando os sinais dos elementos da matriz. Se chamamos uma matriz de A, então a matriz oposta é -A.

Exemplo:

Considere a matriz A a seguir:

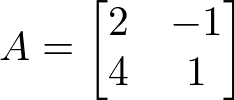
Então a matriz oposta -A é:

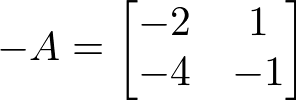
Matriz Transposta

Uma matriz transposta é uma matriz resultante da troca ordenadamente de linhas pelas colunas de outra matriz. Se temos uma matriz A, então a transposta de A tem notação A^t.

Exemplo:

Seja a matriz A = [a_ij]_mxn, a matriz transposta de A é A^t = [a_ij]_nxm.

Propriedade da transposta

Considere as matrizes A e B, e a um número real qualquer, caso as operações a seguir sejam possíveis, então temos que:

• (A + B)^t = A^t + B^t
• (a.A)^t = a.A^t
• (A^t)^t = A
• (A.B)^t = B^t.A^t
• Uma matriz é simétrica, se, e somente se, ela seja igual à sua transposta: A = A^t.
• Uma matriz é antissimétrica, se, e somente se, ela seja igual à oposta da sua transposta: A = -A^t.
• Uma matriz quadrada é ortogonal, se, e somente se, a sua transposta seja igual a sua inversa: A^t = A^-1.

Operações entre Matrizes

Aplicar as operações da aritmética para resolver problemas com matrizes é importante e vamos ver cada um delas a seguir:

Igualdade de Matrizes

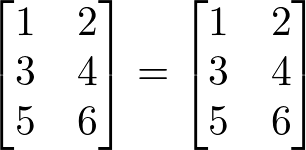
Duas matrizes A e B de mesma ordem mxn são iguais, se, e somente se, todos os elementos que correspondem a B e a A sejam iguais. Ou seja, A = B ⇔ a_ij = b_ij.

Exemplo:

Adição de Matrizes

Para fazer a adição de duas matrizes, devemos somar todos os elementos correspondentes de uma matriz com a outra, ou seja, somar linha com linha e coluna com coluna. As matrizes devem ter a mesma ordem.

Exemplo:

Sejam A e B duas matrizes de mesma mxn. Somamos A e B, e escrevemos A + B, obtendo uma matriz C de mesma ordem mxn, de forma que C seja obtida somando os elementos correspondentes de A e B. Veja:

Propriedades da adição de matrizes

Considerando A, B e C matrizes de mesma ordem e N uma matriz nula, caso as operações a seguir sejam possíveis, então temos que:

• Comutativa: A + B = B + A
• Associativa: (A + B) + C = A + (B + C)
• Elemento neutro: A + N = N + A = A
• Elemento oposto: A + (-A) = (-A) + A = N
• (A + B)^t = A^t + B^t

Subtração de Matrizes

Para fazer a subtração de duas matrizes, devemos subtrair todos os elementos correspondentes de uma matriz com a outra, ou seja, subtrair linha com linha e coluna com coluna. As matrizes devem ter a mesma ordem.

Exemplo:

Sejam A e B duas matrizes de mesma ordem mxn. Fazemos a diferença de A e B, e escrevemos A – B, obtendo uma matriz C de mesma ordem mxn, de forma que C seja obtida subtraindo os elementos correspondentes de A e B. Veja:

Multiplicação de um número real por uma Matriz

Seja A_mxn uma matriz, e a um número real. O produto de a por A resulta em uma matriz B_mxn, de forma que multiplicamos o número real a por cada elemento de A.

Exemplo:

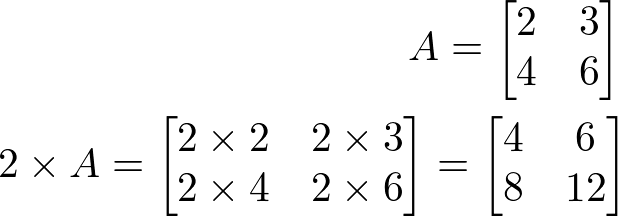
Propriedades

Considerando A e B matrizes de mesma ordem e a e b números reais, caso as operações a seguir sejam possíveis, então temos que:

1. 1 . A = A
2. (-1) x A = -A
3. a . 0 = 0
4. 0 . A_mxn = 0_mxn
5. a . (b . A_mxn) = (a . b) . A_mxn
6. a . (A + B) = a . A + a . B
7. (a + b) . A = a . A + b . A

Multiplicação entre Matrizes

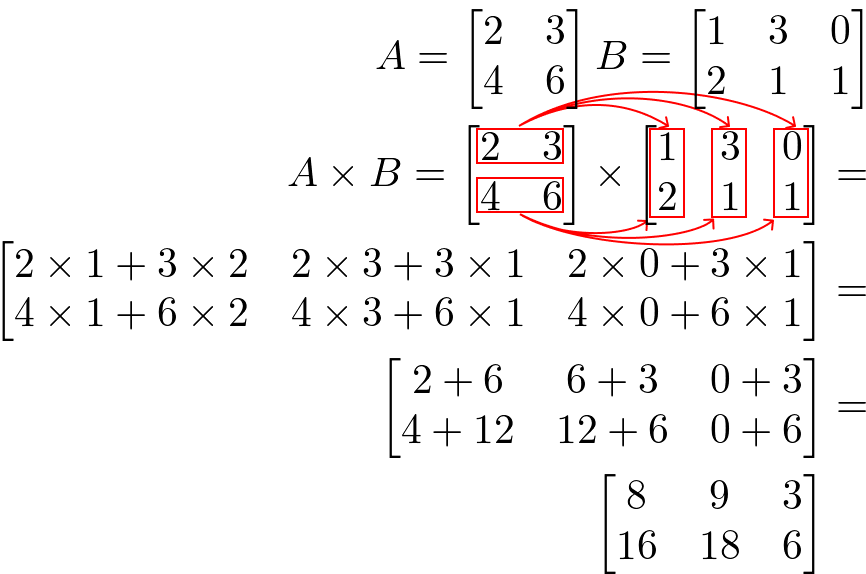
Considerem as matrizes A_mxn e B_nxp. A multiplicação das matrizes A e B, nesta ordem, resulta em C_mxp, de forma que C seja obtida pela soma dos produtos dos elementos da linha i de A e da coluna j de B.

Exemplo:

Considerem as matrizes A e B, então A x B é:

Observações importantes:

1. A multiplicação de matriz somente é possível se o número de colunas em uma matriz for igual ao número de linhas da outra matriz.
2. A matriz resultante C tem o mesmo número de linha da primeira matriz e o mesmo número de colunas da segunda matriz.

Matrizes e Determinantes

O determinante de uma matriz A é um número real indicado por det A.

Determinantes de matrizes de ordem 1, 2 e 3

Determinante de uma matriz de ordem 1 é o próprio elemento.

A = [a] ⇒ det A = a

Determinante de uma matriz de ordem 2

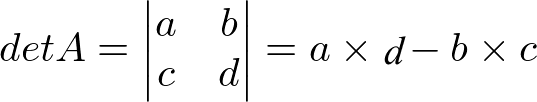
Determinante de uma matriz de ordem 3

Para matrizes de ordem 3, deve-se aplicar a regra de Sarrus para calcular o determinante. Este método só se aplica para matrizes de ordem 3.

Considere a matriz A quadrada de ordem 3:

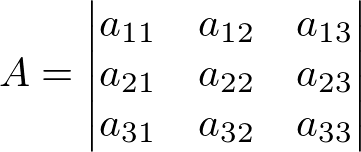
Copiamos a 1ª e a 2ª coluna para a direita da matriz:

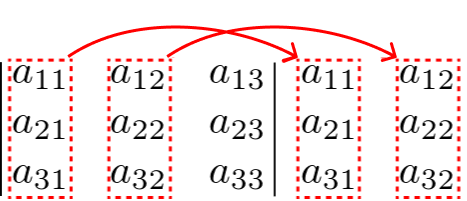
Após isso, multiplicamos os termos entre si, seguindo as setas abaixo, colocando o sinal como especificado na imagem:

det A = a₁₁ . a₂₂ . a₃₃ + a₁₂ . a₂₃ . a₃₁ + a₁₃ . a₂₁ . a₃₂ – a₁₃ . a₂₂ . a₃₁ – a₁₁ . a₂₃ . a₃₂ – a₁₂ . a₂₁. a₃₃

A ideia é multiplicar os elementos no sentido das setas e colocar os respectivos sinais de adição e subtração como está especificado.

Determinante de matrizes de ordem superior a 3

Para matrizes de ordem superior a 3, devemos utilizar o teorema de Laplace. Antes de falarmos sobre o teorema de Laplace é preciso entendermos o que é cofator ou complemento algébrico (M_ij).

Cofator ou complemento algébrico (M_ij)

Para calcularmos o cofator ou complemento algébrico de um elemento a_ij, em uma matriz M de ordem n, com n > 1, devemos utilizar a seguinte fórmula:

M_ij = (-1)^{i + j} . D_ij

Onde i e j são os índices do elemento em questão, e D_ij representa o determinante da matriz resultante com a eliminação das linhas e colunas para o elemento escolhido.

Exemplo:

Vamos calcular o cofator M₂₃ para a matriz abaixo:

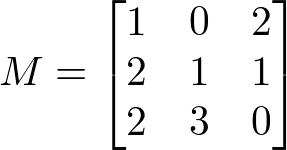
Então, escolhemos o elemento M₂₃ e removemos a linha e coluna em relação a ele. Temos:

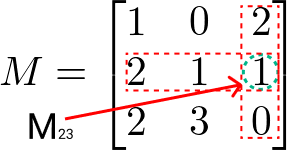
Agora aplicaremos a fórmula definida acima. Assim:

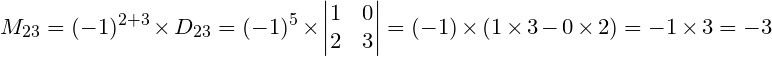
Aplicamos a fórmula e calculamos o determinante D₂₃ para a matriz resultante, depois que excluímos a linha e coluna para o elemento da posição M₂₃.

Teorema de Laplace

O teorema de Laplace pode ser aplicado em matrizes de ordem n, com n > 1. Mas como vimos nos tópicos anteriores, existem regras mais adequadas para cálculos dos determinantes de matrizes de ordem menores que 4.

Para facilitar o cálculo utilizando o teorema de Laplace, devemos escolher uma linha ou coluna com a maior quantidade de zeros possíveis, pois isso ajuda na hora do cálculo. Isto é, teremos menos trabalhos para fazer a conta.

Exemplo:

Considere a matriz A a seguir:

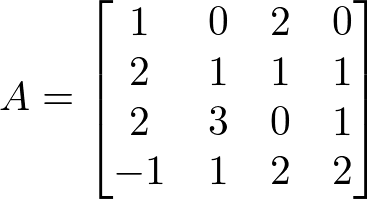
Resolução:

Olhando a matriz A, vamos escolher a primeira linha como referência, pois temos um número maior de zero e isso nos ajudará a fazer menos cálculos.

Assim:

det (A) = a₁₁ . A₁₁ + a₁₂ . A₁₂ + a₁₃ . A₁₃ + a₁₄ . A₁₄ = 1 . (–1)^{1 + 1} . D₁₁ + 0 . (–1)^{1 + 2} . D₁₂ + 2 . (–1)^{1 + 3} . D₁₃ + 0 . (–1)^{1 + 4} . D₁₄ = D₁₁ + 2D₁₃

Agora temos que determinar as matrizes D₁₁ e D₁₃, removendo as linhas e colunas para os elementos da posição D_ij.

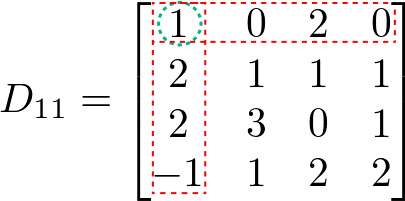
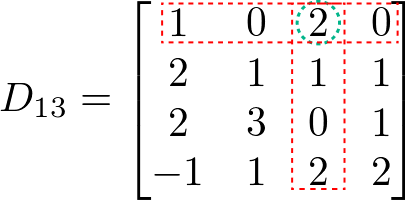
Então:

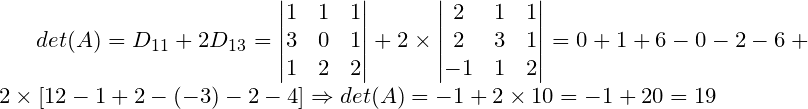
Portanto, det (A) = 19

Acima calculamos o determinante para D₁₁ e D₁₃ utilizando a regra de Sarrus para matrizes de ordem 3.

Exercícios

Treine seus conhecimentos resolvendo os exercícios propostos acessando link a seguir:

• Exercícios com matrizes

Bons estudos!

Leia também…

• Matriz Identidade
• Matriz Transposta
• Matrizes e Determinantes
• Matriz Inversa