Matrizes e Determinantes são conceitos fundamentais na resolução de problemas envolvendo equações matriciais.
O determinante de uma matriz quadrada M é a associação de um número real único, chamado de determinante de M e podemos abreviar por det (M), que pode ser utilizado na resolução de sistemas lineares.
Notação para determinantes de matrizes
Seja a matriz M a seguir:
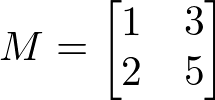
Definimos determinantes de M como det (M) ou
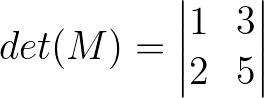
Determinante de matriz de ordem 1
O determinante de uma matriz de ordem 1×1 é o próprio elemento da matriz.
Exemplo:
- A = [1] ⇒ det A = 1
Determinante de matriz de ordem 2
O determinante das matrizes quadradas — aquelas que possuem os mesmo números de linhas e colunas — de ordem 2×2 é calculado pela multiplicação dos elementos da diagonal principal e secundária. Assim:
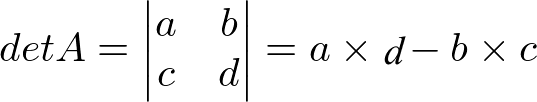
Exemplo:
Seja a matriz M:
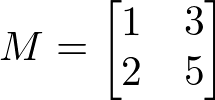
Então:
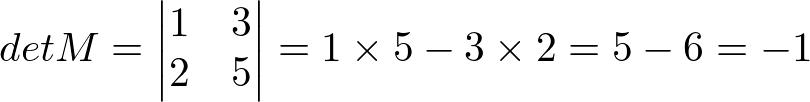
Determinantes de matriz de ordem 3
Para calcularmos o determinante de uma matriz quadrada de ordem 3×3 temos que utilizar a regra de Sarrus. Veja como:
Seja A uma matriz quadrada de ordem 3×3:
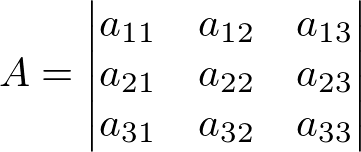
A regra de Sarrus funciona da seguinte maneira:
Copiamos a 1ª e 2ª coluna da matriz A para o lado
direito da matriz, veja:
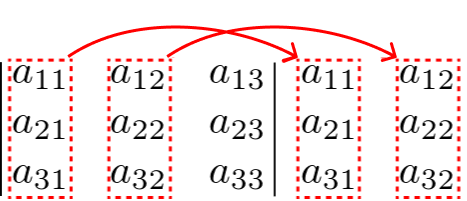
Depois fazemos o produto entre os termos da matriz com as colunas que copiamos para o lado direito, seguindo as setas abaixo: para as setas azuis, multiplicamos os 3 elementos diagonalmente e associamos os sinais de mais (+); para as setas vermelhas, multiplicamos os 3 elementos de cada seta e associamos o sinal de menos (-). Veja:

Então: det A = a11 . a22 . a33 + a12 . a23 . a31 + a13 . a21 . a32 – a13 . a22 . a31 – a11 . a23 . a32 – a12 . a21. a33
Vamos ver um exemplo prático.
Exemplo:
Considere a matriz A abaixo:

Assim, seguindo a regra de Sarrus, copiamos a 1ª e 2ª coluna de A para o lado direito:

Seguindo o sentido das setas e obedecendo os sinais, temos que:
det A = 1 . 5 . 3 + 3 . 1 . 2 + 0 . 2 . 1 – 0 . 5 . 2 – 1 . 1 . 1 – 3 . 2 . 3 = 15 + 6 + 0 – 0 – 1 – 18 = 21 – 19 = 2
Portanto, det(A) = 2
Determinante para matrizes de ordem 4 ou superior
Para calcularmos o determinante de matrizes de ordem igual ou superior a 4×4, devemos utilizar o teorema de Laplace para o cálculo do determinante dessas matrizes.
É importante lembrar que o teorema de Laplace pode ser aplicado em matriz de ordem nxn, com n > 1, porém, matriz de ordem 2×2 e 3×3, as regras anteriores ensinadas são mais eficientes, isto é, dão menos trabalho para calcular.
Antes de mostrarmos o teorema de Laplace precisamos entender alguns conceitos que precisamos saber para entender o teorema.
Menor complementar (Dij)
O menor complementar de um elemento aij, em uma matriz A, é obtido eliminando a linha i e coluna j de aij. Dessa forma, teremos uma matriz de ordem n – 1, e o determinante Dij dessa matriz é o menor complementar do elemento aij.
Exemplo:
Seja A, a matriz abaixo:

Calcule os menores complementares D11 e D21.
Resolução:
Para D11, eliminamos a linha e coluna correspondente para o elemento a11:

Temos a matriz:

Então D11 é: det(A) = 5 . 3 – 1 . 1 = 15 – 1 = 14
Para encontrarmos D21, eliminamos a linha e coluna correspondente para o elemento a21:

Assim, temos a matriz:

Então D21 é: det(A) = 3 . 3 – 0 . 1 = 9 – 0 = 9
Cofator ou complemento algébrico (Aij)
Chamamos de cofator ou complemento algébrico de um elemento aij, para matrizes de ordem n, isto é, matrizes quadradas, um número Aij, de forma que:
Aij = (-1)i + j . Dij
Exemplo:
Seja a matriz A, a seguir, calcule A22 e A13:

Resolução:
Cofator para A13:
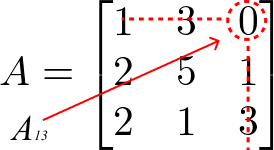
Vamos aplicar a fórmula: Aij = (-1)i + j . Dij
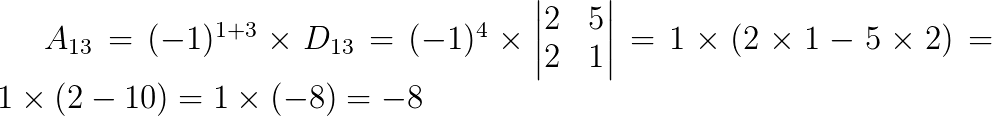
Cofator para A22:
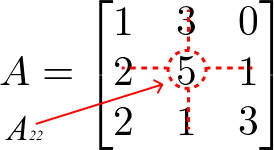
Aplicando a fórmula: Aij = (-1)i + j .
Dij
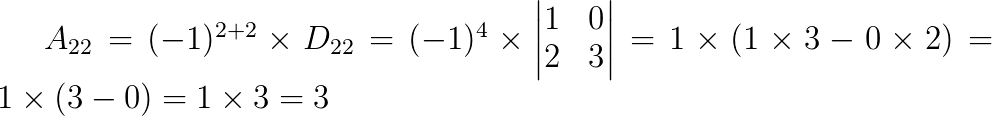
Bom, agora que já sabemos calcular o menor complementar e o cofator, podemos estudar o teorema de Laplace.
Teorema de Laplace
Com o teorema de Laplace podemos encontrar o determinante de uma matriz quadrada A da seguinte forma:
- Devemos escolher uma linha ou coluna aleatoriamente;
- Somar os produtos dos elementos da linha ou coluna que escolhemos pelos seus cofatores;
- O determinante de A é o resultado encontrado no item 2.
Exemplo:
Seja matriz quadrada A a seguir:

Pela matriz A, devemos escolher a primeira linha pois contém mais 0 (zeros) e isso nos ajudará a fazer um número menor de cálculos.
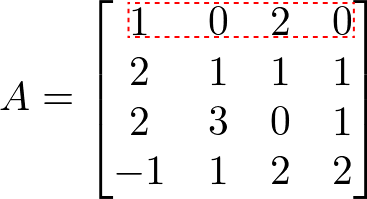
Então, devemos multiplicar os elementos da linha escolhida pelos seus cofatores:
Assim:
det (A) = a11 . A11 + a12 . A12 + a13 . A13 + a14 . A14 = 1 . (–1)1 + 1 . D11 + 0 . (–1)1 + 2 . D12 + 2 . (–1)1 + 3 . D13 + 0 . (–1)1 + 4 . D14 = D11 + 2D13
Como escolhemos uma linha com maior quantidade de zeros, isso anulou, durante a multiplicação, alguns cálculos.
Após isso, vamos calcular os cofatores para os elementos D11 e D13:
Para D11, removendo a linha e
coluna do elemento:

Temos a seguinte matriz:
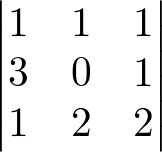
Para D13, removendo a linha e
coluna do elemento:

Temos a seguinte matriz:
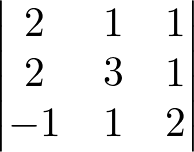
O determinante para as matrizes D11 e D13 foi calculado utilizando a regra de Sarrus para matrizes de ordem 3.

det(D11) = (1 . 0 . 2) + (1 . 1 . 1) + (1 . 3 . 2) – (1 . 0 . 1) – (1 . 1 . 2) – (1 . 3 . 2) = 0 + 1 + 6 – 0 – 2 – 6 = 7 – 8 = -1

det(D13) = (2 . 3 . 2) + (1 . 1 . (-1)) + (1 . 2 . 1) – (1 . 3 . (-1)) – (2 . 1 . 1) – (1 . 2 . 2) = 12 – 1 + 2 – (-3) – 2 – 4 = 17 – 7 = 10
Por fim, D11 + 2 . D13 = -1 + 2 . 10 = -1 + 20 = 19
Portanto, det(A) = 19
Propriedades das matrizes e dos determinantes
- O determinante de uma matriz quadrada A é igual ao determinante da sua transposta: det (A) = det (At);
- Caso exista uma linha ou coluna na matriz igual a zero, o determinante é zero;
- Caso exista duas filas paralelas, iguais ou proporcional, o determinante é zero;
- O determinante do produto de um número real k por uma matriz A é igual ao produto de k elevado a n, onde n é o número de linhas de A, pelo determinante de A: det (k . A) = kn . det (A);
- Caso os elementos abaixo ou acima da diagonal principal forem nulos, o determinante será o produto dos elementos da diagonal principal;
- Teorema de Binet: Seja A e B matrizes quadradas de ordem n, o determinante do produto de A por B é igual ao produto dos determinantes de A e B.
Exercícios
Resolva os exercícios propostos acessando o link abaixo:
Bons estudos!
Leia também…



