Calcule os determinantes das matrizes dos exercícios a seguir. Responda às questões e consulte as respostas após para checar.
1) Considere a matriz abaixo de ordem 2, calcule o seu determinante:

Ver resposta
O determinante de uma matriz de ordem 2 é calculado multiplicando os elementos da diagonal principal com os elementos da diagonal secundária.
Portanto,
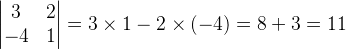
2) Seja a matriz A de ordem 3, calcule o seu determinante:

Ver resposta
Matrizes de ordem 3 podemos calcular o determinante usando a regra de Sarrus. Assim:
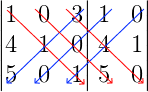
(1 x 1 x 1) + (0 x 0 x 5) + (3 x 4 x 0) – (5 x 1 x 3) – (0 x 0 x 1) – (1 x 4 x 0) = -14
Portanto, o det(A) = – 14
3) Considere a matriz B de ordem 4, calcule o seu determinante:
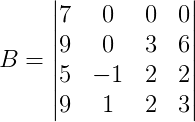
Ver resposta
Podemos calcular o determinante para matrizes de ordem 4 ou superior utilizando o teorema de Laplace.

Podemos escolher qualquer linha, mas vamos escolher a primeira, pois tem mais zeros.
Logo:
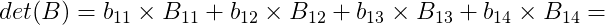
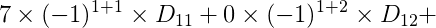
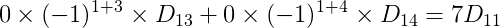
Agora vamos calcular o cofator para D11. Removendo a linha e coluna correspondente da matriz B, temos a seguinte matriz.
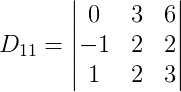
Agora vamos calcular o determinante para D11, como temos uma matriz de ordem 3 podemos utilizar a regra de Sarrus. Assim:
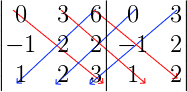
det(D11) = (0 x 2 x 3) + (3 x 2 x 1) + (6 x (-1) x 2) – (1 x 2 x 6) – (2 x 2 x 0) – (3 x (-1) x 3) = -9
Por fim, temos que:
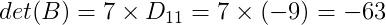
Espero que estes exercícios tenham ajudado a entender como calcular determinantes de matrizes.


