Responda os exercícios abaixo para entender como calcular a matriz inversa de uma matriz qualquer.
1) Considerem as matrizes a seguir:
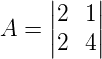
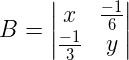
Sabendo que B é a matriz inversa de A, e x e y são números reais. Calcule o produto entre x e y.
Ver resposta
Como B é a inversa de A, temos que o produto entre A e B é igual a matriz identidade.
Assim, temos: A x B = I
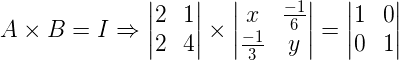
Resolvendo o produto entre as matrizes temos:
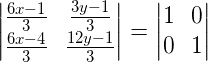
Logo,
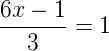
6x – 1 = 3
6x = 3 + 1
x = 4/6
x = 2/3
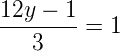
12y – 1 = 3
12y = 3 + 1
y = 4/12
y = 1/3
Portanto, o produto entre x e y é:
x . y = 2/3 . 1/3 = 2/9
2) Seja a matriz A a seguir, determine  .
.
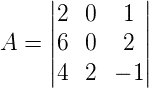
Ver resposta
Antes de determinar a inversa de uma matriz, temos que verificar se ela é inversível. Uma matriz é inversível quando seu determinante é diferente de zero.
Utilizando a regra de Sarrus para encontrar o determinante de A, temos:
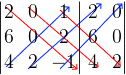
det(A) = 2 x 0 x (-1) + 0 x 2 x 4 + 1 x 6 x 2 – 4 x 0 x 1 – 2 x 2 x 2 – (-1) x 6 x 0 = 4
Como det(A) > 0, temos que A é inversível e podemos determinar  .
.
Sabe-se que
A .  = I
= I
Então:
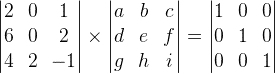
Como não sabemos qual é a inversa de A, atribuímos variáveis a  . Dessa forma, temos que resolver para achar os valores destas
variáveis.
. Dessa forma, temos que resolver para achar os valores destas
variáveis.
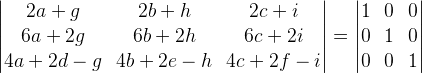
Assim, temos o seguinte sistema de equações:
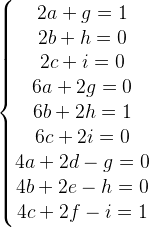
Resolvendo o sistema:
2a + g = 1 ⇒ g = 1 – 2a ⇒ g = 1 – 2(-1) = 3
2b + h = 0 ⇒ h = -2b ⇒ h = -2(1/2) = -1
2c + i = 0 ⇒ i = -2c ⇒ i = -2(0) = 0
6a + 2g = 0 ⇒ 6a + 2(1 – 2a) = 0 ⇒ 6a + 2 – 4a = 0 ⇒ 2a + 2 = 0 ⇒ 2a = -2 ⇒ a = -2/2 = -1
6b + 2h = 1 ⇒ 6b + 2(-2b) = 1 ⇒ 6b – 4b = 1 ⇒ 2b = 1 ⇒ b = 1/2
6c + 2i = 0 ⇒ 6c + 2(-2c) = 0 ⇒ 6c – 4c = 0 ⇒ 2c = 0 ⇒ c = 0
4a + 2d – g = 0 ⇒ 4(-1) + 2d – 3 = 0 ⇒ 2d – 7 = 0 ⇒ d = 7/2
4b + 2e – h = 0 ⇒ 4(1/2) + 2e – (-1) = 0 ⇒ 2 + 2e + 1 = 0 ⇒ 2e = – 3 ⇒ e = – 3/2
4c + 2f – i = 1 ⇒ 4(0) + 2f – 0 = 1 ⇒ 2f = 1 ⇒ f = 1/2
Portanto, substituindo os valores nas variáveis, temos que a inversa de A é:
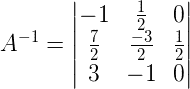
3) Determine a inversa de M.

Ver resposta
Vamos primeiramente verificar se M é inversível. Pela regra de Sarrus, temos que:
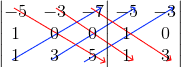
det(M) = (-5) x 0 x 5 + (-3) x 0 x 1 + (-7) x 1 x 3 – 1 x 0 x (-7) – 3 x 0 x (-5) – 5 x 1 x (-3) = – 6
Logo, como M é inversível, pois det(M) > 0, vamos determinar a inversa de M.
Então:
M . 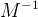 = I
= I
Assim:
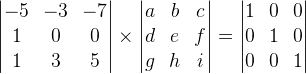
Resolvendo o produto, temos então:
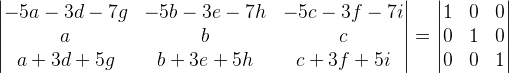
Agora temos que resolver o seguinte sistema:

Vamos lá, temos
a = 0
b = 1
c = 0
b + 3e + 5h = 0 ⇒ 1 + 3e + 5h = 0 ⇒ 3e = – 1 – 5 h ⇒ e = (- 1 – 5h)/3 ⇒ e = (-1 – (5.(-2)))/3 ⇒ e = (- 1 + 10) / 3 ⇒ e = 9/3 ⇒ e = 3
-5b – 3e – 7h = 0 ⇒ -5(1) – 3(- 1 – 5h)/3 – 7h = 0 ⇒ – 5 + 1 + 5h – 7h = 0 ⇒ – 4 – 2h = 0 ⇒ – 2h = 4 ⇒ – h = 4/2 ⇒ h = – 2
c + 3f + 5i = 1 ⇒ 0 + 3f + 5i = 1 ⇒ 3f = 1 – 5i ⇒ f = (1 – 5i)/3 ⇒ f = (1 + 5/2)/3 ⇒ f = (7/2)/3 ⇒ f = 7/6
-5c – 3f – 7i = 0 ⇒ – 3(1 – 5i)/3 – 7i = 0 ⇒ – 1 + 5i – 7i = 0 ⇒ – 2i = 1 ⇒ i = – 1/2
a + 3d + 5g = 0 ⇒ 0 + 3d + 5g = 0 ⇒ 3d = – 5g ⇒ d = – 5g/3 ⇒ d = (-5(-1/2))/3 ⇒ d = (5/2)/3 ⇒ d = 5/6
-5a – 3d – 7g = 1 ⇒ -3(-5g)/3 – 7g = 1 ⇒ 5g – 7g = 1 ⇒ – 2g = 1 ⇒ g = – 1/2
Portanto, temos que a inversa de M é:
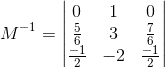
4) Seja a matriz
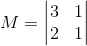
, verifique se a matriz
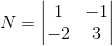
Ver resposta
Para determinar se uma matriz é a inversa de outra matriz, o produto 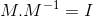 . Ou seja, M . N = I.
. Ou seja, M . N = I.
Assim, temos que:
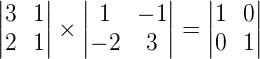
Fazendo o produto, temos então que:
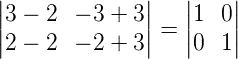
Dessa forma, chegamos a uma igualdade:
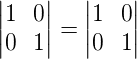
Portanto, podemos concluir que N é a matriz inversa de M.
é a inversa de M.
Quando praticamos respondendo os exercícios sobre matriz inversa, facilmente conseguimos aprender a resolver qualquer questão Assim, o segredo é praticar. Bons estudos!
Mais exercícios sobre matrizes que servem para ajudar na resolução de questões sobre matriz inversa.


