Sistema de Equações: Veja Como Resolver

Chamamos sistema de equações duas ou mais equações que formam um conjunto onde as equações se relacionam com as mesmas incógnitas.

Além disso, um sistema é formado por equações do primeiro grau quando todas as equações possuem grau 1 e as equações tenham duas incógnitas diferentes em cada uma delas.

Exemplo:

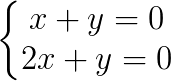
Como resolver um sistema de equações do 1º grau?

Para resolver um sistema de equações do 1º grau existem dois métodos: método da substituição e o método da adição.

Método da substituição

Nessa método, escolhemos uma das equações do sistema, isolamos uma das variáveis da equação escolhida e substituímos na outra equação.

Exemplo:

Considere o sistema:

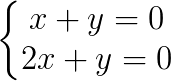
Enumeremos as equações:

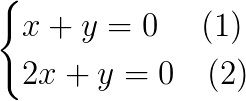
Escolhemos a equação 1 e isolamos uma das variáveis:

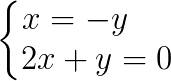
Isolamos o x da equação 1, agora vamos substituir na equação 2:

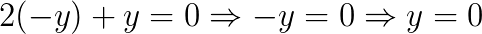
Nesse passo, já descobrimos o valor de y, agora vamos encontrar o valor de x, então devemos substituir o valor de y na equação x = -y.

x = -y ⇒ x = 0

Portanto, a solução do sistema é S = {0, 0}.

Vamos ver outro exemplo:

Considere o sistema abaixo:

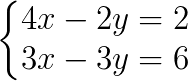
Enumeramos as equações:

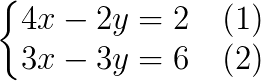
Vamos isolar o x na equação 2:

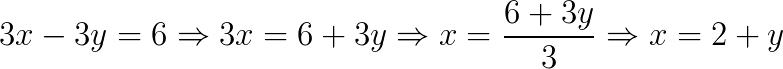
Agora vamos substituir x na equação 1: 4x – 2y = 2:

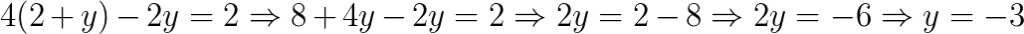
já encontramos o valor de y, agora vamos voltar e substituir em x = 2 + y:

x = 2 – 3 ⇒ x = -1

Portanto, o conjunto solução do sistema é: S = {-1, -3}

Método da adição

O método da adição consiste em somar uma equação com a outra, para isso é preciso que as incógnitas somadas tenham o mesmo valor e sinal contrário.

Exemplo:

Considere o sistema:

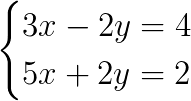
O sistema já possui duas incógnitas com sinais trocados, então basta somá-las.

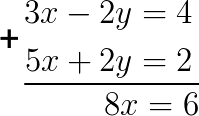
Como agora a equação só tem uma incógnita, podemos encontrar o valor dela:

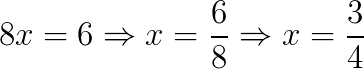
Por fim, vamos escolher uma das equações do sistema e substituir o valor de x.

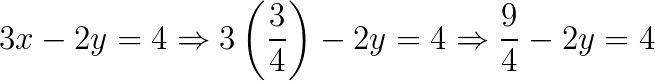
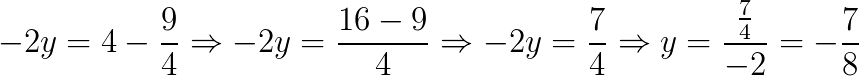
Portanto, o conjunto solução do sistema é: S = {³⁄₄; –⁷⁄₈}

Dúvidas com frações? Estude o MMC e divisão de frações.

Vamos ver mais um exemplo:

Considere o sistema:

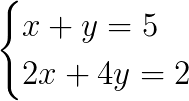
Não podemos somar o sistema como está, pois, não eliminaremos nenhuma incógnita. Para isso, devemos multiplicar a primeira equação por -2, toda ela.

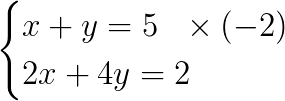
Fazendo isso, temos o seguinte sistema:

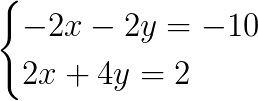
Agora podemos somar às duas equações:

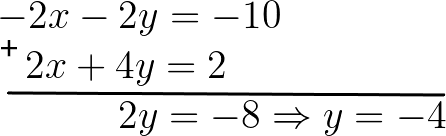
Com o valor de y, vamos escolher uma das equações do sistema e substituir para encontrar o valor de x.

Substituindo y = -4 em x + y = 5, temos:

x – 4 = 5 ⇒ x = 5 + 4 ⇒ x = 9

Portanto, o conjunto solução do sistema é: S = {9; -4}

Classificação dos Sistemas de Equações

Os sistemas de equações do primeiro grau têm a seguinte forma: a₁x + b₁y = c₁ e a₂x + b₂y = c₂ e podem ser classificados como:

1. Possível e determinando;
2. Possível e indeterminando;
3. Impossível.

Possível e determinando: um sistema é possível e determinando quando possui somente uma solução, então:

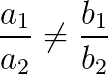
Possível e indeterminando: um sistema é possível e indeterminando quando possui infinitas soluções, então:

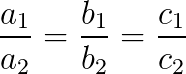
Impossível: um sistema é impossível quando não possui nenhuma solução, então:

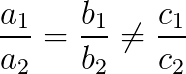
Exemplo:

Considere o sistema abaixo e classifique-o em possível e determinado, possível e indeterminando ou impossível:

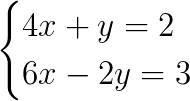
Vamos calcular as razões para poder classificar o sistema:

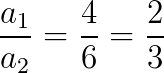
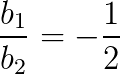
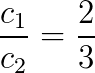
Como

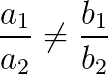
O sistema é possível e determinado.

Exercícios

Os exercícios podem ser acessados no link a seguir:

• Exercícios com sistema de equações