Aprenda a resolver equações usando sistema de equações com os exercícios a seguir. Resolva e consulte as respostas no final.
1) Resolva em R o sistema a seguir utilizando o método da substituição:
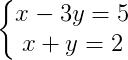
Ver resposta
Devemos começar enumerando as equações:
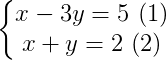
Depois escolha uma equação para isolar uma das variáveis, vamos escolher a equação 2:
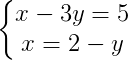
Agora vamos substituir x na primeira equação:
x – 3y = 5 ⇒ 2 – y – 3y = 5 ⇒ – 4y = 5 – 2 ⇒ – 4y = 3 ⇒ y = – 3/4
Para achar o valor de x vamos substituir em x = 2 – y.
x = 2 – y ⇒ x = 2 – (- 3/4 ) ⇒ x = 2 + 3/4 ⇒ x = (8 + 3) / 4 ⇒ x = 11/4
Portanto, o conjunto solução do sistema é S = {- 3/4, 11/4}
2) Numa fazenda são criados gados e galinhas, num total de 200 cabeças e 500 pés. Determine o total de gado e galinhas.
Ver resposta
Atribuindo variáveis a gado (x) e galinhas (y), logo o sistema montado é:
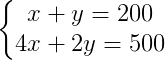
Obs.: Gado possui 4 patas e galinhas 2 patas, ambos possuem 1 cabeça.
Isolando o x:
x = 200 – y
Substituindo x na segunda equação, temos:
4x + 2y = 500 ⇒
4(200 – y) + 2y = 500 ⇒
800 – 4y + 2y = 500 ⇒
– 2y = 500 – 800 ⇒
– 2y = – 300 ⇒
y = 300/2 ⇒
y = 150
Substituindo y em x = 200 – y, temos então:
x = 200 – 150 ⇒
x = 50
Portanto, o total de gados é 50 e de galinhas é 150.
3) Se um número x é o dobro de y e a soma deles é 30, quais são os números x e y?
Ver resposta
Montando o sistema, temos:
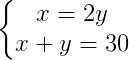
Substituindo x em x + y = 30, então:
2y + y = 30 ⇒
3y = 30 ⇒
y = 30/3 ⇒
y = 10
Substituindo y em x = 2y para encontrar o valor de x, logo:
x = 2(10) ⇒
x = 20
Portanto, os valores de x é 20 e de y é 10.
4) Resolva em R o sistema a seguir usando o método da adição.
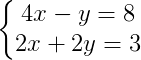
Ver resposta
Vamos multiplicar a primeira equação por 2.
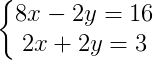
Agora podemos somar a primeira equação com a segunda, pois elas possuem duas variáveis iguais com sinais diferentes.
Somando às duas equações chegamos a seguinte equação:
10x = 19
Logo:
x = 19/10
Agora basta escolhermos uma equação do sistema e substituir o valor de x que encontramos:
2(19/10) + 2y = 3 ⇒
38/10 + 2y = 3 ⇒
2y = 3 – 38/10 ⇒
2y = (30 -38)/10 ⇒
2y = – 8/10 ⇒
y = – (8/10)/2 ⇒
y = – 8/20
Portanto, o conjunto solução do sistema é S = {19/10, – 8/20 }
5) Determine se o sistema abaixo possui solução em R:
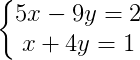
Ver resposta
Um sistema de equações do primeiro grau tem a seguinte forma:
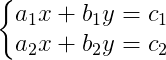
Um sistema é possível e determinado se:
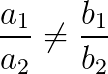
Logo:
a1 / a2 = 5/1 = 5
b1 / b2 = 9/4
Portanto, como
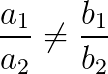
O sistema é possível e determinado, ou seja, possui solução em R.


