Teste seus conhecimentos respondendo os exercícios a seguir sobre sistemas lineares.
1) Resolva o sistema abaixo utilizando a regra de Cramer:
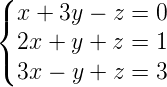
Ver resposta
Na regra de Cramer calculamos o determinante principal e depois os secundários substituindo a coluna das variáveis pela coluna dos termos independente.
Vamos lá, para o sistema da questão temos a seguinte matriz associada:
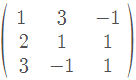
Vamos calcular o determinante usando a regra de Sarrus. Assim, calculando o determinante principal desta matriz, temos:
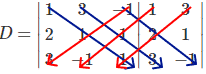
det(D) = 1 . 1 . 1 + 3 . 1 . 3 + (-1) . 2 . (-1) – 3 . 1 . (-1) – (-1) . 1 . 1 – 1 . 2 . 3 = 10
Agora vamos calcular o determinante secundário Dx, antes devemos substituir toda a coluna do x pela coluna do termo independente. Assim:
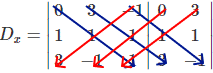
det(Dx) = 0 . 1 . 1 + 3 . 1 . 3 + (-1) . 1 . (-1) – 3 . 1 . (-1) – (-1) . 10 -1 . 1 . 3 = 10
Próximo passo é calcular o determinante Dy, antes vamos substituir a coluna y pela coluna do termo independente. Então:
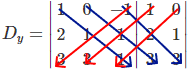
det(Dy) = 1 . 1 . 1 + 0 . 1 . 3 + (-1) . 2 . 3 – 3 . 1 . (-1) – 3 . 1 . 1 – 1 . 2 . 0 = – 5
Por fim, vamos calcular o determinante secundário Dz, antes vamos substituir a coluna z pela coluna do termo independente. Logo:
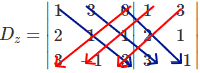
det(Dz) = 1 . 1 . 3 + 3 . 1 . 3 + 0 . 2 . (-1) – 3 . 1 . 0 – (-1) . 1 . 1 – 3 . 2 . 3 = – 5
Dessa forma, podemos achar os valores de x, y e z fazendo:
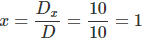
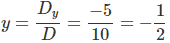
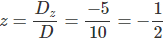
Portanto, a solução do sistema é: x = 1, y = z = – 1/2
2) Determine o valor de x no sistema abaixo, utilize a regra de Cramer:
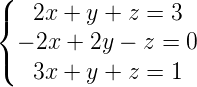
Ver resposta
Vamos utilizar a regra de Sarrus para calcular o determinante principal.
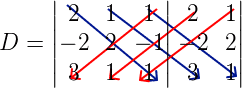
Assim, det(D) = 2 . 2 . 1 + 1 . (-1) . 3 + 1 . (-2) . 1 – 3 . 2 . 1 – 1 . (-1) . 2 – 1 . (-2) . 1= -3
Vamos calcular agora o determinante secundário Dx, substituindo a coluna do x pelo termo independente. Veja!

det(Dx) = 3 . 2 . 1 + 1 . (-1) . 1 + 1 . 0 . 1 – 1 . 2 . 1 – 1 . (-1) . 3 – 1 . 0 . 1 = 6
Próximo passo é calcular o determinante secundário para Dy, substituindo a coluna do y pelo termo independente. Assim:
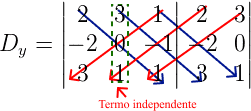
det(Dy) = 2 . 0 . 1 + 3 . (-1) . 3 + 1 . (-2) . 1 – 3 . 0 . 1 – 1 . (-1) . 2 – 1 . (-2) . 3 = -3
Por fim, o determinante secundário para Dz, substituindo a coluna do z pelo termo independente. Logo:
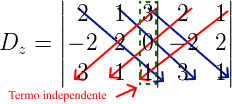
Então, det(Dz) = 2 . 2 . 1 + 1 . 0 . 3 + 3 . (-2) . 1 – 3 . 2 . 3 – 1 . 0 . 2 – 1 . (-2) . 1 = -18
Com os determinantes principal e secundário calculados podemos encontrar os valores de x, y e z fazendo:
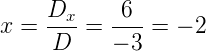
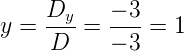
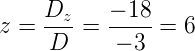
Portanto, a solução do sistema é: x = -2, y = 1 e z = 6
3) Usando escalonamento, resolva o sistema a seguir:
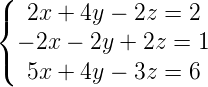
Ver resposta
Utilizando escalonamento para resolver o sistema, temos os seguintes passos:
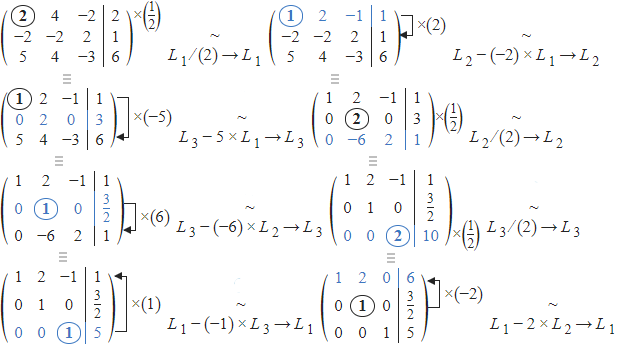
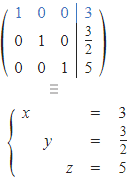
Portanto, a solução do sistema é: x = 3, y = 3/2 e z = 5
Imagens: (https://matrixcalc.org/pt/)
4) Se x, y e z são a solução do sistema linear:
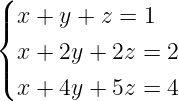
Determine o produto entre x, y e z.
Ver resposta
A matriz associada ao sistema é:
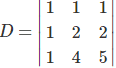
Calculando o determinante principal, temos que
det(D) = 1 . 2 . 5 + 1 . 2 . 1 + 1 . 1 . 4 – 1 . 2 . 1 – 4 . 2 . 1 – 5 . 1 . 1 = 1
O determinante secundário Dx é:
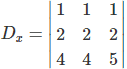
Temos que det(Dx) =1 . 2 . 5 + 1 . 2 . 4 + 1 . 2 . 4 – 4 . 2 . 1 – 4 . 2 . 1 – 5 . 2 . 1 = 0
O determinante secundário Dy é:
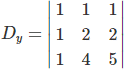
Logo, det(Dy) = 1 . 2 . 5 + 1 . 2 . 1 + 1 . 1 . 4 – 1 . 2 . 1 – 4 . 2 . 1 – 5 . 1 . 1 = 1
Por fim, o determinante secundário Dz é:
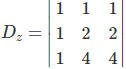
Assim, det(Dz) = 1 . 2 . 4 + 1 . 2 . 1 + 1 . 1 . 4 – 1 . 2 . 1 – 4 . 2 . 1 – 4 . 1 . 1 = 0
Agora que temos o determinante principal e os secundários, vamos calcular os valores de x, y e z, fazendo:
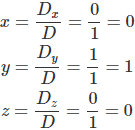
Portanto, a solução do sistema é: x = 0, y = 1 e z = 0; e o produto x . y . z = 0 . 1 . 0 = 0
Mostramos como resolver exercícios com sistemas lineares usando a regra de Cramer e escalonamento, que são as formas mais usuais de resolver sistema.
Pratique resolvendo mais exercícios sobre sistema de equações e matrizes que também ajudam na resolução de sistemas lineares. Acesse:


