A área do triângulo é geralmente calculada através do produto da medida da base do triângulo pela sua altura, e dividido por 2.
O triângulo é um polígono com três lados, este lados são formados por segmentos de retas unidos em três pontos que chamamos de vértices.
No cálculo da área deve-se considerar o tipo de triângulo. Para cada tipo temos uma maneira de identificar as medidas e propriedades necessárias para realizar o cálculo.
Os tipos de triângulos que temos são: triângulo retângulo, equilátero, isósceles e escaleno.
Como calcular a área de um triângulo?
Para a maioria dos triângulos, o cálculo da área segue a seguinte forma: pegamos a medida da base e multiplicamos pela sua altura, dividimos o resultado desse produto por 2.
Dessa forma, para a maioria dos triângulos, usamos a seguinte fórmula:

Onde:
- A: a área;
- b: é a base do triângulo;
- h: é a altura do triângulo.
Importante lembrar que essas letras são convenções usadas na matemática. Se você prefere utilizar outras letras, isso não vai alterar o cálculo.
Área do Triângulo Retângulo
O triângulo retângulo é um tipo especial de triângulo na matemática. Esse triângulo é chamado de retângulo porque possui um ângulo reto, isto é, um ângulo que mede 90°. Além disso, possui dois ângulos agudos, ou seja, ângulo que mede menos que 90°.
Ademais, possui também dois ângulos agudos, ou seja, ângulos que medem menos que 90°.
Dependendo da forma como está posicionado o triângulo retângulo, a sua altura pode ser igual a um dos seus lados. Veja na imagem abaixo:

E a área é o produto entre a base e a altura, dividido por 2.
Área do Triângulo Equilátero
O triângulo equilátero é um dos tipos de triângulo que existe e tem esse nome porque possui todos os lados e ângulos internos com as mesmas medidas.
No triângulo equilátero, a altura (h) do triângulo divide o triângulo em dois, dessa forma teremos dois triângulos.
O lado que representa a base podemos chamá-lo de (l), e será dividido em dois pela altura. Logo o lado da base será l / 2.
Agora para encontrar a medida da altura vamos utilizar o teorema de Pitágoras, assim:

Por fim, para determinarmos a fórmula que calcula a área do triângulo equilátero, precisamos utilizar o Teorema de Pitágoras para encontrar a medida da altura.
Assim, devemos substituir o valor da altura (h) encontrado na fórmula geral. Então temos:

Onde:
- A: é a área;
- l: representa os lados do triângulo.
Área do Triângulo Isósceles
O triângulo isósceles é um tipo de triângulo que possui dois lados e dois ângulos com as mesmas medidas. A fórmula para calcular a área de um triângulo isósceles é a mesma fórmula para os casos gerais: o produto da base pela altura, dividido por 2.
No cálculo da área, às vezes, o valor da altura não é especificado na questão. Assim, temos que utilizar o Teorema de Pitágoras para calcular a altura antes de utilizar a fórmula geral.
Exemplo:
Seja o triângulo a seguir:

Resolução:
No triângulo acima, conhecemos somente as medidas relativas aos seus lados, no entanto, para o cálculo da área de um triângulo precisamos conhecer o valor da sua altura. Para isso vamos utilizar o Teorema de Pitágoras. Assim:

Veja que a altura divide o triângulo em dois, então a medida que representa um dos lados do triângulo no teorema, neste caso, será a metade do triângulo original.
Após encontrarmos o valor da altura, podemos utilizar a fórmula geral e calcular a área do triângulo isósceles.
Área do Triângulo Escaleno
O triângulo escaleno é um tipo de triângulo que possui todos os lados e ângulos com medidas diferentes. Para encontrar a área para esse tipo de triângulo, devemos utilizar os nossos conhecimentos em trigonometria.
Exemplo:
Considere o triângulo ABC abaixo, a altura h foi traçada com relação ao lado b definido como base:

A altura h, calculada a partir do triângulo amarelo, é: h = c . sen(A).
Dessa forma, substituindo o valor da altura na fórmula geral do triângulo, temos:
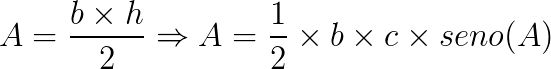
Se considerarmos os outros lados do triângulo escaleno, teremos:

Espero que tenha ficado claro, bons estudos e boa sorte.
Exercícios
Acesse os exercícios no link a seguir:


