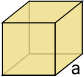
O cubo é um poliedro regular contendo 6 faces com as mesmas medidas. As arestas também possuem as mesmas medidas e são perpendiculares.

O cubo é considerado um sólido de Platão. Os poliedros regulares estudados pela escola de Platão apresentam as seguintes características:
- As faces são formadas por polígonos regulares e congruentes, no caso do cubo o polígono regular é o quadrado;
- Os vértices possuem 3 arestas cada um;
- Apresentam ângulos congruentes, isto é, com a mesma medida;
- O número de vértices (V), o número de arestas (A) e o número de faces (F), vale a seguinte relação de Euler: V – A + F = 2
O cubo é um poliedro da geometria espacial. Isto quer dizer que ele utiliza às três coordenadas x, y e z. Os poliedros da geometria plana utilizam apenas as coordenadas x e y. Isto faz do cubo uma figura tridimensional, ou 3D como queira chamar.
Elementos de Formação
Os elementos que formam esta figura geométrica são os seguintes:
- Arestas: possui 12 arestas, essas arestas são segmentos de retas congruentes;
- Faces: é formado também por 6 faces quadrangulares, cada face do é um polígono regular, mais especificamente um quadrado.
- Diagonais: é possível traçar até quatro diagonais internamente no cubo. Além disso, as faces também possuem suas diagonais.
- Vértices: os vértices são formados por pontos onde as arestas se encontram, no total o cubo possui 8 vértices.
- Ângulos: nos vértices, ângulos retos são formados, no total o cubo possui 24 ângulos retos.
Área
A área de um objeto ou figura geométrica é a medida equivalente a sua superfície. No caso da área do cubo, existem três áreas importantes: a área da base, a da lateral e a total.
Área da base: a área da base é equivalente a calcular a área de um quadrado, já que as faces são formadas por quadrados. Logo, a fórmula da área da base é:

Ab = a²
Onde:
- Ab: é a área da base;
- a: a medida da aresta.
Área lateral: a área lateral equivale a calcular a medida das faces que não são bases (a face de cima e a de baixo, são as bases). Assim, a fórmula para a área lateral é:
Al = 4a²
Onde:
- Al: é a área da base;
- a: a medida da aresta.
Como a lateral é composta por quatro faces, onde essas faces são quadrados, precisamos apenas calcular a área de um quadrado e multiplicar por 4.
Área total: a área total é a medida referente a toda a superfície. Dessa forma, como o cubo tem 6 faces, precisamos calcular a área de uma face e multiplicar o resultado por 6. Então, temos a seguinte fórmula:
At = 6a²
Onde:
- At: é a área da base;
- a: a medida da aresta.
Leia mais sobre como é o cálculo da área.
Volume
Para calcular o volume não há a necessidade de pegar a medida de todas as arestas. Como o cubo é o poliedro regular, as faces e arestas possuem medidas iguais. Dessa forma, precisamos apenas pegar a medida de uma aresta.
O volume é calculado utilizando três medidas: comprimento, largura e altura.
Como as arestas têm as mesmas medidas, então o comprimento, a largura e a altura do cubo são iguais. Dessa forma, precisamos apenas da medida de uma aresta e elevá-la a potencia de 3.
Então, chegamos a seguinte fórmula:
V = a³
Onde:
- V: é a medida do volume;
- a: é a medida da aresta.
Lembrete: a unidade de medida do cubo é o metro cúbico (m³), por ser uma medida tridimensional, assim: m . m . m = m³
Leis mais sobre como calcular o volume.
Diagonais
O cubo possui dois tipos de diagonais: digonal da base e a diagonal do cubo.
- Diagonal da base: a diagonal da base é a medida equivalente à diagonal de um quadrado. A face é um quadrado como já sabemos. Assim, a diagonal da base do cubo é encontrada utilizando o Teorema de Pitágoras. Então, temos a seguinte fórmula: db² = a² + a² ⇒ db² = 2a² ⇒ db = a√2
- Diagonal: é a medida de um segmento de reta traçado de um vértice a outro do cubo, atravessando-o ao centro. Também podemos encontrar a medida dessa diagonal utilizando o Teorema de Pitágoras. Assim, temos a seguinte fórmula para calcular a diagonal interna: dc² = a² + d²b ⇒ dc² = a² + 2a² ⇒ dc² = 3a² ⇒ dc = a√3
Leis mais sobre a diagonal do cubo.
Exercícios
Acesse os exercícios no link abaixo:


