Poliedro é uma figura espacial fechada formada por polígonos reunidos que formam as suas faces. As faces são os lados, formadas por arestas unidas nos vértices.

Existem duas categorias de poliedros: convexos e não convexos:
Convexo: é convexo quando dois pontos que formam um segmento de reta na
superfície está inteiramente contido no poliedro;
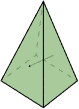
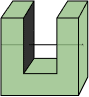
Côncavo ou não convexo: é côncavo quando dois pontos que formam um
segmento de reta nas extremidades e parte deste segmento de reta não pertença ao
poliedro.
Definição de Poliedro Convexo
Seja um poliedro com um número n, com n ≥ 4, de polígonos convexos, de forma que:
- Dois polígonos do poliedro não pertença ao mesmo plano;
- Cada lado de um polígono no poliedro é comum a somente dois polígonos;
- Cada plano de uma face deixa os demais polígonos das outras faces no mesmo semiespaço;
Dessa forma, temos n semiespaços que possuem origem no plano de um polígono da face que contem os demais.
Assim, o poliedro convexo é denominado pela intersecção dos n semiespaços.
Elementos de um poliedro
Os poliedros convexos são formados pelos seguintes elementos:
- Faces: as faces são formadas por polígonos convexos;
- Arestas: as arestas são os lados dos polígonos das faces;
- Vértices: os vértices são os mesmos dos polígonos das faces;
- Superfícies: as superfícies do poliedro são a reunião das faces.
Poliedros de Platão
Denominamos um poliedro de Platão se ele atende aos seguintes requisitos:
- As faces possuem o mesmo número de arestas;
- Nos vértices partem o mesmo número de arestas;
- Vale a relação de Euler (V – A + F = 2).
Os 5 Poliedros de Platão
Os poliedros de Platão são nomeados em apenas cinco classes:
| Nome | m | n | A | V | F |
|---|---|---|---|---|---|
| Tetraedro | 3 | 3 | 6 | 4 | 4 |
| Hexaedro | 3 | 4 | 12 | 8 | 6 |
| Octaedro | 4 | 3 | 12 | 6 | 8 |
| Dodecaedro | 3 | 5 | 30 | 20 | 12 |
| Icosaedro | 5 | 3 | 30 | 12 | 20 |
Legenda:
- m: Número de arestas que parte do vértice
- n: Número de aresta da face
- A: Arestas
- V: Vértices
- F: Faces

Relação de Euler para poliedro convexo
Segundo Euler, em todos os poliedros convexos valem a seguinte relação:
V – A + F = 2 ou F + V = 2 + A
Onde:
- V: é o número de vértices;
- A: é o número de arestas;
- F: é o número de faces.
Essa relação do Teorema de Euler é válida para poliedros convexos, nos quais as faces são formadas por polígonos regulares com o mesmo número de arestas. Também pode ser válida para alguns poliedros não convexos.
Classificação dos poliedros
São classificados em regulares e não regulares:
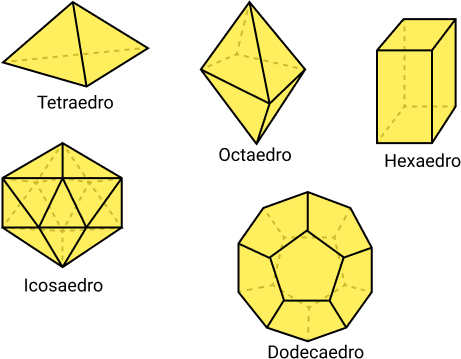
Regulares: são os poliedros em que suas faces são formadas por polígonos regulares e congruentes:
- Tetraedro: o tetraedro é um poliedro com 4 faces triangulares;
- Hexaedro: 6 faces quadrangulares;
- Octaedro: 8 faces triangulares;
- Dodecaedro: 12 faces pentagonais;
- Icosaedro: 20 faces triangulares.
Os poliedros são nomeados conforme o número de faces que possuem. Como, por exemplo:
- Hexaedro: 6 faces, 8 vértices e 12 arestas;
- Tetradecaedro: 14 faces, 16 vértices e 28 arestas;
- Dodecaedro: 12 faces, 20 vértices e 30 arestas.
Podemos determinar o número de vértices e arestas analisando as faces do poliedro e aplicar relação de Euler: V + F = A + 2.
Exemplo:
- Dodecaedro: 12 faces pentagonais, cada face possui 5 arestas. Então: A = (12 . 5) / 2 = 30 arestas. Aplicando a relação de Euler: V + F = A + 2 ⇒ V + 12 = 30 + 2 ⇒ V = 32 – 12 ⇒ V = 20.
- Tetraedro: 6 faces triangulares, cada face possui 3 arestas. Logo: A = (6 . 3) / 2 = 18 / 2 = 9. Agora encontramos o número de vértices: V + 6 = 9 + 2 ⇒ V = 11 – 6 ⇒ V = 11 – 6 = 5.
Não Regulares: são os poliedros em que suas faces são formadas por polígonos regulares e não regulares:
- Prisma: é uma figura geométrica espacial com duas bases congruentes, uma inferior e a outra superior. As faces são formadas por quadriláteros ou paralelogramos.
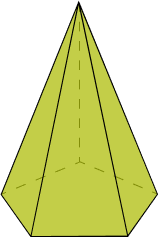
- Pirâmide: a pirâmide é uma figura geométrica espacial formada por uma base poligonal e faces triangulares unidas em um vértice que não pertence ao plano da base.
Exercícios
Veja os exercícios no link abaixo:



